At least year’s Bridges Conference in Stockholm, I attended a short presentation by Susan Goldstine about “self-diagramming lace”. As motivation for the new work she was presenting, Susan referenced her paper from the year before on what she calls “symmetry samplers”. Samplers are an old tradition in fibre arts. A symmetry sampler combines small swatches depicting every possible mathematical pattern type that can be realized in a given medium.
As an example, Susan showed a picture of Mary Shephard’s piece “Wallpapers in Cross-Stitch”:

If you are familiar with repeating two-dimensional patterns, you will know that there are precisely 17 distinct pattern types, known as wallpaper groups. This sampler shows only 12. But as Susan pointed out in her talk, Shephard’s piece is nevertheless a complete symmetry sampler. In cross-stitch, the stitches are applied to a woven fabric (called “aida”), which has holes for stitches arranged in a square lattice. Rectangular grids are fundamental to woven cloth, and necessarily constrain the symmetries that are achievable in cross-stitch. In particular, the square grid cannot support threefold or sixfold rotations (consider, for example, that no three points in a square lattice can form an equilateral triangle), which prohibits the five wallpaper groups that include them (for the record, they are p3, p31m, p3m1, p6, and p6m in the traditional crystallographic notation).
But hang on a minute. The restriction to 12 groups follows directly from the structure of the aida, not from a mathematical law. And while it’s certainly true that almost every cloth on earth is woven using warp and weft at right angles to each other, producing a rectangular arrangement of holes, other weaves are possible. I started thinking about an article I had worked on in my past capacity as editor of Journal of Mathematics and the Arts: Paul Gailiunas’s study of the mathematical properties of mad weave:

Mad weave is triaxial: it’s made from threads in three evenly spaced directions. And look at the arrangement of holes left behind:
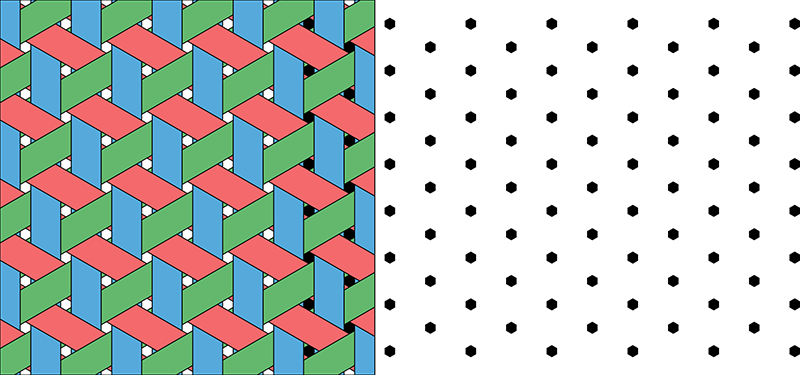
With a suitable stitching pattern, those holes would permit threefold and sixfold rotational symmetries!
Sitting in Susan’s talk, these two threads came together (so to speak). If I could find (or make) a suitable piece of triaxial cloth, I could use it as a kind of aida. Then I’d have to develop a new stitching pattern that’s as analogous as possible to traditional cross-stitch. At that point, I’d be able to create a hexagonal cross-stitch symmetry sampler. I resolved to attempt this project in time for the following year’s Bridges conference.
Obviously, the cloth would have to be very fine, so that stitches on it would be sufficiently small. I wasn’t eager to weave that myself by hand. So first, I looked into the manufacturing of woven triaxial fabrics. It turns out that they do exist. They have good engineering properties: they tend to be more isotropic than regular woven cloth (they behave similarly in every direction) and less stretchy (because they don’t shear). After a lot of exploration, I reached out to Sakase Adtech in Japan. They very generously sent me a few samples of their polyester triaxial fabrics. The weave they use is actually not the same as mad weave; it’s what Paul Gailiunas called “open hexagonal weave” in his article. But the large hexagonal holes in that weave are still in the correct arrangement:

I had never done any cross-stitching before, so I thought it would be prudent to start by creating a traditional square piece. I adapted a small piece of pixel art I had created a couple of years ago for a laptop sticker, leading to my first ever cross-stitch project:

I made a bunch of mistakes in transcribing the pattern, and you should see the horrific mess in back. But it provided a suitable introduction to the medium, enough to get working on the hexagonal piece.
I needed to develop a stitching pattern that would produce little units as similar as possible to the X that forms the units of traditional cross-stitch. After experimenting with and rejecting a few alternatives, I settled on this pattern:
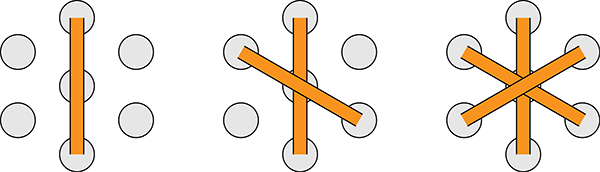
Here, three individual stitches in a prescribed order (“vertical, backslash, slash”) make up an asterisk-shaped unit. The stitches begin in the six hexagonal holes surrounding another hexagon and jump over that central hole, meaning that a number of holes have no stitches in them. That’s fine, of course, if the units are small enough, and this approach turns out to be the most convenient way to work with this fabric.
It was then time to design patterns. I decided to divide the sampler into a kind of hexagonal honeycomb (to emphasize the sixfold symmetry), and I created vector drawings in Illustrator for every cell. Each drawing shows the low-level hexagonal holes of the fabric, with larger, filled-in hexagons showing the intended units:
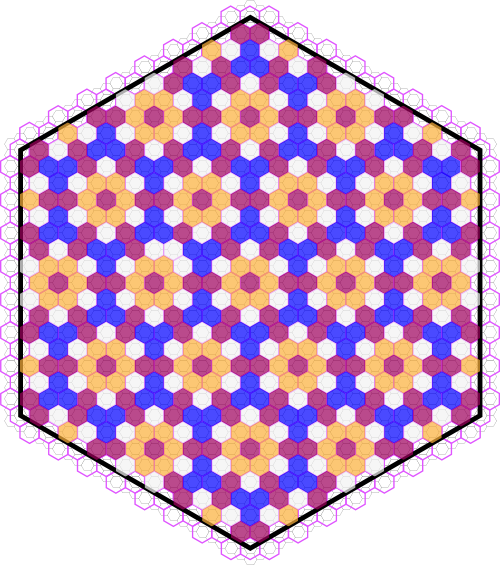
With all those pieces in place, the last step was very simple: hours upon hours of punishing, tedious manual labour. My close-up vision has taken a sharp nosedive in the past couple of years, so here I was aided by a very stylish magnifying visor with built-in LED headlamp. I’m quite happy with the finished result:
There are five large hexagonal cells, containing the five symmetry groups that are not possible using traditional cross-stitch: reading in rows from the top, p31m, p3m1, p3, p6, and p6m. The other three cells are each divided into three rhombi, showing the other nine wallpaper groups that are also possible with hexagonal holes: p1, p2, pm, pg, cm, pmg, pgg, pmm, and cmm. This fabric can’t show fourfold rotations, which leaves precisely three wallpaper groups (pm, p4g, and p4m) on the sewing room floor. That makes for a grand total of 14 groups, versus 12 for traditional cross-stitch. Take that, Mary Shephard!
A pedantic mathematician will no doubt observe that the sampler doesn’t actually have all the symmetries advertised here. In each individual unit, the stitches are layered, which strictly speaking eliminates nearly all possible kinds of symmetry. Pedant, I salute you! Indeed, if you take the layering of threads into account, and require every unit to follow the vertical-backslash-slash pattern, then I think you’re able to represent only groups p1 and p2. Of course, the same layering problem arises with traditional cross stitch, and we respond with the same simplification: for the purpose of evaluating symmetry we flatten stacks of thread into conceptual blobs of colour.
Very special thanks to Ryoji Sakai and Sakase Adtech for sending me samples of their triaxial fabrics, and to Teruhisa Sugimoto for providing assistance in reaching out to them. Thanks also to Veronika Irvine for providing feedback on both the mathematical and stitching sides of this project, and to Linda Carson for suggesting the oddly shaped matte, which was expertly cut by The Artstore in Waterloo. And of course, thanks to my wife Nathalie for teaching me the basics of cross-stitch, giving me access to her large stash of supplies, and not mocking my visor too much.



Leave a Reply to Craig Kaplan Cancel reply