Craig S. Kaplan and Doris Schattschneider

Abstract

In the 1970s, Branko Grünbaum and Geoffrey C. Shephard developed an algebraic notation to describe the structure of shapes that tile the plane isohedrally and used their notation to derive a complete set of 93 isohedral tiling types. Their notation subsumes the older categorization developed by Heinrich Heesch and Otto Kienzle in the 1960s, and the extension to that notation developed by Hans-Günther Bigalke and Heinrich Wippermann in the 1990s. Nevertheless, those alternative notations are still used in some parts of the design world and are useful when creating tile shapes. We offer a complete cross-reference table that relates these various notations and illustrates each isohedral type with a representative tile and its tiling.

Introduction

A tiling of the plane is isohedral if its tiles form a single transitivity class under the symmetries of the tiling. That is, every tile in the tiling has the same shape, and for every two tiles A and B, there exists a symmetry of the tiling that maps A to B. Put even more simply, the tiles are “all the same”: there’s nothing about any tile’s shape, or its placement relative to the rest of the tiling, to distinguish it from any other tile. Isohedral tilings are quite practical in art and design: nearly all of Escher’s famous regular divisions of the plane can be understood in terms of isohedral tilings. They are also easy to represent and manipulate in software.

In the twentieth century, several mathematicians studied the problem of enumerating all the different ways that a shape can tile in regular ways (where in hindsight, we can take “regular” to mean “isohedral”). These various analyses make different assumptions about what tile shapes ought to be considered, and how tiles are permitted to be arranged in a tiling; the result is different lists of “tiling types”. The enumeration by Branko Grünbaum and Geoffrey C. Shephard, first published in 1977 [3] and later included as Section 6.2 of Tilings and Patterns [4], is the most discriminating: it yields the largest number of distinct tiling types (the 93 IH Types). Other classifications can be regarded as either picking out a subset of those types with specific properties, or lumping sets of types together by ignoring the distinctions made by Grünbaum and Shephard.

Still, other systems for describing isohedral tiles have endured. In particular, some designers and some drawing tools continue to use notation introduced by Heinrich Heesch and Otto Kienzle [5], which is arguably easier to work with by hand than Grünbaum and Shephard’s incidence symbols. We refer to these as the 28 HK Types.

Because of the continued use of multiple classification systems, we thought it would be helpful to compile a new cross-reference table showing how they relate to each other. In Grünbaum and Shephard’s original article [3] they included a column relating IH Types to the work of other authors, including the HK Types. However, that article may be somewhat obscure, particularly to non-mathematicians, and the column in question contains a small number of errors. Schattschneider’s book [6] includes a table relating IH and HK Types, but only for the subset of types that were used by Escher in his tesellations. In this short report we offer a comprehensive table relating IH and HK Types. For good measure we also include the notation developed by Hans-Günther Bigalke and Heinrich Wippermann [1], the 43 BW Types, which are intermediate between the other two in their ability to discriminate isohedral tilings. We will briefly describe the three methods of classification and the notations they use (in order of increasing complexity), and then present our annotated, interactive table.

The Heesch-Kienzle (HK) Types

Heesch and Kienzle were interested in classifying shapes with the property that a tiling by that shape had the shape itself as a fundamental region. Such a shape is generically asymmetric (because if its tiling forced symmetries upon it, those symmetries would divide it into multiple fundamental regions). They also ignored tilings containing lines of mirror reflection, whether through the bodies of tiles or along boundaries between neighbouring tiles.

In their 1963 book Flächenschluß [5], they presented a shorthand notation that describes the boundary of a prototile, divided up into curves (edges) at its tiling vertices (places where three or more tiles meet in the tiling). The notation consists of a “word” of three to six letters with optional subscripts. Each letter labels an edge of the tile, indicating an isometry that carries that edge to another edge of the tile. The letters are interpreted as follows:

• A T denotes translation: the tile will be adjacent to a translated copy of itself. Thus the word will necessarily contain another T on the “opposite” side of the tile, where that translated copy will meet the present tile. Most HK types that contain a T contain exactly two of them, making their relationship clear. The two exceptions are TTTT and TTTTTT; in these cases, each edge is related to the one exactly halfway around the tile, but these different pairs are otherwise unrelated.
• A C denotes rotation, with an optional subscript depending on the order of rotation. A C without a subscript represents an S-shaped curve, i.e., an edge that is symmetric under a halfturn (a 180° rotation) about its centre. A C with a subscript of 3, 4, or 6 represents one of two edges on the tile’s boundary that meet at a vertex with that order of rotational symmetry. For example, in a word containing …C₃C₃…, the tangents of the two C₃ edges will meet at an angle of 120°. Another way to describe it is that the first edge labeled C₃ will rotate by 120° about its vertex to create the second C₃ edge.
• A G denotes glide reflection: the tile will be adjacent to a copy of itself that has been translated and reflected across a glideline parallel to the direction of translation. The word will necessarily contain a corresponding G, whose edge will be the glide-reflected image of the first G. Here, subscripts are sometimes necessary for distinguishing between different glide-reflections; otherwise we would not be able to distinguish TG₁G₁TG₂G₂ from TG₁G₂TG₂G₁, for example.

Heesch and Kienzle’s classification results in 28 tiling types, each with an associated word. The types are conventionally numbered HK1–HK28 according to the numbering they give in Table 10 of Flächenschluß (the table takes the form of an insert that folds out from the book). Here we offer our own redrawn version of the table as a scalable vector PDF, which you are free to download and re-use.

Every shape described by the HK types necessarily tiles the plane isohedrally, but their classification omits many other isohedral types. These are types in which the prototile is forced to be symmetric, and/or the tiling’s symmetry group contains reflections. In Grünbaum and Shephard’s table of isohedral types, the subset corresponding to HK types are those for which the induced tile group is c1 and the symmetry group of the corresponding tiling has no reflections (i.e., it is one of the seven wallpaper groups p1, p2, p3, p4, p6, pg, or pgg).

The Bigalke-Wippermann (BW) Types

In 1994, Bigalke and Wippermann published Reguläre Parkettierungen [1], which discusses the mathematics of “regular” (i.e., isohedral) tilings with applications to manufacturing, art, and design. It also includes a concrete presentation of computational methods (in BASIC) for drawing these tilings.

In the first chapter of their book, they enumerate what they call the “simple tilings” (einfacher Parketts). These are intermediate between the 28 HK types and the full set of isohedral types: every tile must still be a fundamental region of its tiling’s symmetry group (meaning that the prototile is asymmetric), but the symmetry group is permitted to include reflections. These correspond to all types listed by Grünbaum and Shephard that have an induced tile group of c1. There are 46 such types, but three of them cannot be realized with unmarked tiles and are therefore considered inadmissible by Bigalke and Wippermann. Thus their list contains 43 types, which we denote BW1–BW43 in the order given in Section 1.6 of their book.

Their word-based notation is essentially identical to that of Heesch and Kienzle, with the addition of one new letter:

• An S denotes mirror reflection (spiegelung). This tile edge will be a straight line, and the tiling contains a mirror reflection across that line. The edge will therefore be the shared edge between neighbouring tiles.

In their book, Heesch and Kienzle also discuss the use of a symbol S to denote mirror reflections, but they do not classify tiles whose boundaries incorporate reflections.

Bigalke and Wippermann also sometimes give a word that is rotated relative to that of Heesch and Kienzle; for example, HK21 is CGG and BW3 is GGC, which describe the same tiling type. Their enumeration contains one special case: BW9, which has word SSS. This tiling type represents a triangular tile with copies reflected across each of its three edges; there are three distinct topological types that support a triangular tiling of this type, corresponding to IH77, IH80, and IH87.

Later, in Section 5.3 of their book, they give a complete enumeration of the 93 isohedral tiling types classified by Grünbaum and Shephard. Their list (which they denote RP1–RP93) is a permutation of Grünbaum and Shephard’s types. Because this enumeration does not introduce a novel family of types, we omit it here.

The Grünbaum-Shephard isohedral (IH) Types

In their 1977 paper [3] and 1987 book [4], Grünbaum and Shephard introduce a systematic, algebraic notation that captures the relationships between the curves (edges) that make up the boundary of the prototile of an isohedral tiling.

An isohedral tiling type is summarized using an incidence symbol made out of two words: the tile symbol and the adjacency symbol. The tile symbol describes the boundary of one tile. Here each edge is assigned a symbolic label (a, b, c, …), given in sequential order around the tile, some annotated with a + or –. Edges that are related via a symmetry of the tiling are given the same label. If that symmetry incorporates a reflection, the labels are given opposite signs; if a reflection maps the edge to itself, it is unsigned. The adjacency symbol describes the relationship between a tile and its neighbours. The labelling of a tile is copied to that tile’s neighbours, revealing which label and sign can be found across each a edge, each b edge, and so on. The adjacency word lists these neighbour symbols, one per unique edge label in the main tile, with + and – used when the neighbour is a direct or reflected copy of the original tile. The incidence symbol combines the tile and adjacency symbols, and summarizes one isohedral tiling type when paired with a topological type (represented by one of the 11 Laves tilings). If a topological type is not specified, the incidence symbol can be ambiguous: the three isohedral types IH77, IH80, and IH87 share the symbol [a⁺b⁺c⁺;a^–b^–c^–], just as they share the BW notation SSS, but have three different topologies.

The algebraic nature of this notation made it possible for Grünbaum and Shephard to write down every possible incidence symbol and check which ones corresponded to isohedral tilings. They found 93 distinct isohedral types, which they denoted IH1–IH93. For each one, they chose the lexicographically first incidence symbol among all possible variations for that type.

Of these isohedral types,12 cannot be expressed using the boundaries of the tiles alone. In these cases all tile edges act as mirrors, forcing those edges to be straight lines. As a result, the tiles are forced to be too symmetric to express the specific symmetries implied by the incidence symbol. For these types, Grünbaum and Shephard augmented the tiles with internal markings that reduced their symmetries. The patterned tilings that are produced by the markings are in accord with the incidence symbols. Setting aside these marked isohedral types, Grünbaum and Shephard refer to the 81 types that remain as the isohedral tiling types.

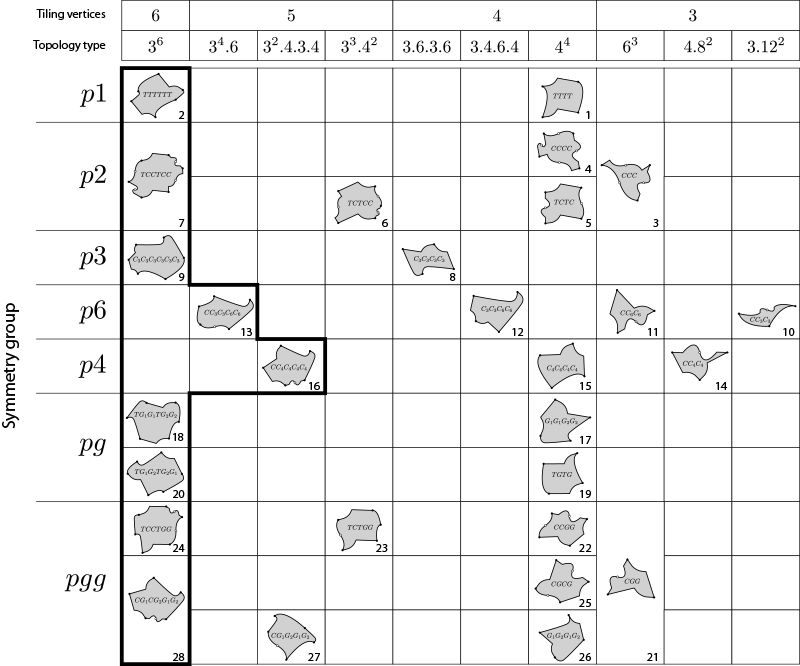
The Table

The table below shows all correspondences between IH, HK, and BW types. It contains the following columns. Some columns include interactive features, which are described in italics in the list below.

• IH #: Grünbaum and Shephard’s isohedral tiling type. Click on this column heading to sort the table by IH type.
• Topo.: The topology type of tilings by this type, as exemplified by one of the 11 Laves tilings [4, Section 2.7].
• Incidence symbol: The Grünbaum and Shephard incidence symbol for this isohedral type.
• HK #: When applicable, the Heesch and Kienzle type for this isohedral type. Click on this column heading to sort the table by HK type.
• HK sym.: When applicable, the word describing tiles of this HK type.
• BW #: When applicable, the Bigalke and Wippermann type for this isohedral type. Click on this column heading to sort the table by BW type.
• BW sym.: When applicable, the word describing tiles of this BW type.
• Sample: A thumbnail illustration of a prototile of this type. Click on the thumbnail to open a pop-up drawing of a tiling generated by this prototile.
• Tile sym.: The cyclic or dihedral symmetry group that tiles belonging to this type must possess. Grünbaum and Shephard refer to this group as the induced tile group.
• Tiling sym.: The wallpaper symmetry group of tilings by this type. The group is given first in crystallographic notation [7], and then underneath that in orbifold notation [2].

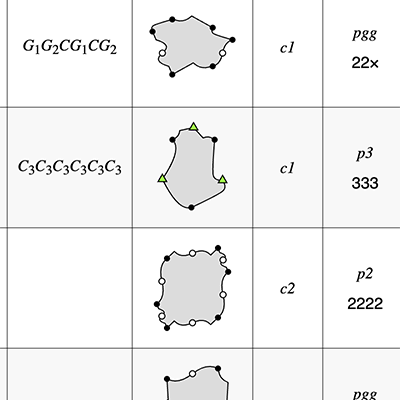
Every representative prototile is annotated as follows:

• Black dots represent generic tiling vertices.
• Green triangles, blue squares, and red hexagons represent tiling vertices where 3-, 4-, or 6-fold rotational symmetry is used in the construction of the tile outline. For example, when a vertex is marked with a triangle, the two edges incident to that vertex will be congruent under a 120° rotation about that vertex (corresponding to …C₃C₃… appearing in the HK or BW symbol for that tiling type).
• White dots are positioned at the centres of tiling edges with twofold (180°) rotational symmetry.
• Tile edges drawn in bold lie on lines of reflection in the tiling and must be straight.
• For tiling types that require markings, the tile is tinted and a green motif is drawn in the tile to reduce its symmetries. The symmetry group of the tiling takes into account the pattern created by the motifs.

Some tile shapes were inspired by the work of M.C. Escher. Reproductions of Escher’s original drawings can be found in Schattschneider’s book [6] or online. All M.C. Escher artworks are ©️ The M.C. Escher Foundation.

References