In the first post in this series, I introduced the concept of a shape’s Heesch number. In brief, if a shape doesn’t tile the plane, its Heesch number is a measure of the maximum number of times you can surround the shape with layers of copies of itself. (Shapes that do tile are defined to have a Heesch number of infinity.) Shapes with positive, finite Heesch numbers are entertaining mathematical curiosities. Far more mysterious—and infuriating—is the fact that we know of examples of Heesch numbers only up to five, and nothing higher. Learning more about shapes with high Heesch numbers could offer insights into deep unsolved problems in tiling theory.
Absent a comprehensive theory about how large Heesch numbers arise, how might we go about enriching our knowledge of the topic? Here, while the mathematician scratches their head, the computer scientist might offer a pragmatic approach. For, even if we can’t make a general statement about Heesch numbers, we can gather a large amount of data by experiment. Specifically, it’s possible to write a computer program that takes a shape as input and searches systematically for all ways to surround that shape, all ways to surround those surrounds, and so on, eventually determining the shape’s Heesch number by brute force. If we tabulate Heesch numbers of enough families of shapes, we might be able to discern patterns that point us at promising lines of mathematical inquiry.
To be sure, there’s a long tradition in mathematics of gathering enough data to make an educated guess about the behaviour of a function or sequence, and then working towards a proof of that guess. Computers haven’t changed that fact, but they’ve allowed us to gather a lot more data a lot faster. Really, my crack about mathematicians versus computer scientists was more a statement about two mindsets; mathematicians and computer scientists use both of these mindsets all the time.
There’s no systematic way to enumerate all shapes, but we can work with a few special-purpose families. We should begin by restricting our attention to polygons—first, because they’re the easiest shapes to describe in a computer program, and second, because it’s not clear that more exotic shapes, say with curved or fractal boundaries, will help us attain higher Heesch numbers. Having made this restriction, we can immediately skip past triangles and quadrilaterals. They all tile the plane, and therefore have Heesch numbers of infinity. (If you haven’t seen this fact before, it’s a fun exercise to convince yourself that every triangle and every quadrilateral tiles the plane.) Not all pentagons tile, and in fact the canonical example of a shape with non-trivial Heesch number (demonstrated by Heesch in 1968, as shown in the previous post) is a convex pentagon. I have more to say about pentagons and other “generic” polygons, but I will defer that discussion to future posts.
A really convenient source of polygons, one that will be familiar to any recreational mathematician, are the polyforms. These are shapes obtained by gluing together simple polygonal modules along their edges. For example, gluing squares together yields polyominoes. The tetronimoes (made from four squares) are the familiar Tetris pieces; the pentominoes are the source of a classic mathematical puzzle (can you assemble them into a 6×10 rectangle?). The related families of polyhexes and polyiamonds can be constructed by gluing together hexagons and equilateral triangles, respectively. Unlike the vast, open-ended problem of exploring the universe of shapes, polyominoes and other polyforms are ideally suited to systematic enumeration by a computer. A square is the only monomino, and to a first approximation, you can construct all n-ominoes by considering all possible ways of gluing one more square onto every empty spot on the boundary of every (n-1)-omino. (This actually generates large numbers of duplicates; more intelligent algorithms will avoid duplicates via judicious gluing.) But as far as I know, there is no compilation of Heesch numbers of simple polyforms. So, in the search for non-trivial Heesch numbers, we now have a simple, albeit computationally intensive, plan: start enumerating polyominoes and test each one for its Heesch number; stop when your computer succumbs to proton decay. We can’t expect to get up to very high values of n—the number of n-ominoes grows exponentially in n—but with luck we can probe deeply enough to find a few surprises. Ready? Go!
Unlike the vast, open-ended problem of exploring the universe of shapes, polyominoes and other polyforms are ideally suited to systematic enumeration by a computer. A square is the only monomino, and to a first approximation, you can construct all n-ominoes by considering all possible ways of gluing one more square onto every empty spot on the boundary of every (n-1)-omino. (This actually generates large numbers of duplicates; more intelligent algorithms will avoid duplicates via judicious gluing.) But as far as I know, there is no compilation of Heesch numbers of simple polyforms. So, in the search for non-trivial Heesch numbers, we now have a simple, albeit computationally intensive, plan: start enumerating polyominoes and test each one for its Heesch number; stop when your computer succumbs to proton decay. We can’t expect to get up to very high values of n—the number of n-ominoes grows exponentially in n—but with luck we can probe deeply enough to find a few surprises. Ready? Go!
Whoa, not so fast. Earlier, I suggested a simple, brute-force approach to computing a shape’s Heesch number, an algorithm that amounts to “try everything”. But consider what happens if I offer as input a polyomino that tiles the plane. The algorithm can always surround such a shape with more layers, out to infinity, and will therefore run forever, always searching for a point where it exhausts every option. There needs to be a way to halt the search if the shape can be shown to tile the plane, in which case the algorithm can provide the answer “infinity” and move on. In other words, a program for computing Heesch numbers has to be at least as smart as a program for determining tileability!
Fortunately, for simpler polyforms we can sidestep this thorny problem. Over the years, Joseph Myers has studied the tiling-theoretic properties of polyominoes, polyiamonds and polyhexes. His web page contains tables of the different ways that these shapes might tile the plane (a deeply fascinating topic, but beyond the scope of this discussion). For him, shapes that don’t tile are the dross of the process, which he collects into a catch-all “non-tilers” column. Our mission, then, is to tease apart that column, sorting non-tilers into bins by Heesch number. The best part is that Myers provides us with lists of non-tilers to use as a starting point. Thus I can write a relatively simple program to compute Heesch numbers, knowing that all the shapes I feed it have previously been determined not to tile.
Results
Fine, so what do we discover in this process? I haven’t searched beyond very small values of n, but the preliminary results are fun to contemplate. Let’s poke around in this new cabinet of curiosities.
To begin with, it’s well known that all n-ominoes tile the plane for n ≤ 6, meaning that any table of Heesch numbers will begin with blank rows where there are no non-tilers. Things start to get interesting at n = 7. One 7-omino has a hole in it, which we’ll immediately discard as incompatible with the computation of Heesch numbers. Three others are non-tilers. Of these, two have Heesch number 1 and one has Heesch number 0.

These shapes are simple enough that you can work out which is which on paper by attempting to surround each tile. So why give away the answer? I’ll leave it as a fun puzzle. If you want to try it, you can use graph paper or these printable worksheets.
Moving on, the hole-free non-tiling 8-ominoes are a mix of Heesch numbers 0 and 1. Happily, when n = 9, we encounter our first example of a polyomino with Heesch number 2. I present this shape with a demonstration, noting that I’m giving away the solution to one puzzle in Good Fences.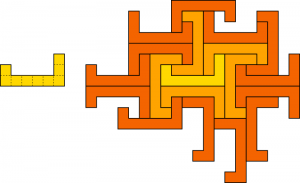
Remember the usual caveats: this diagram doesn’t prove that this shape has Heesch number 2, only that it’s at least 2. It may be possible to find a different configuration that admits another layer of tiles, or perhaps the shape even tiles the plane. In accepting my claim, you are trusting that I am a sufficiently good programmer that my code isn’t missing an opportunity for more surrounds (spoiler: I am, and it’s not). I really like this shape—I feel like it’s a much simpler example of Heesch number 2 than the others we currently have, though of course “simple” is subjective in this context.
As we climb the ladder, each successive value of n becomes harder to resolve in its entirety. Obviously there are exponentially more non-tiling n-ominoes to contend with. Moreover, each one is potentially a more difficult problem: a larger polyomino is likely to have a longer perimeter, meaning more places where you can glue on neighbours, meaning more surrounds (and more partial surrounds too!). It simply takes longer to exhaust all these possibilities. Even worse, my naive algorithm varies wildly in the time it needs to compute a shape’s Heesch number: some shapes take a fraction of a second, others can days hours or days. It’s very hard for a search algorithm to make intelligent decisions about how to direct its search to minimize the work needed, and in any case some shapes just have lots more surrounds than others. So, for example, my program took 1,038,150 seconds, or about 12 days, to decide that the shape on the left has a Heesch number of 1, and it’s still working on the shape on the right after more than 10 days. Stand by!

The table below summarizes what I know so far about polyominoes, just for the record. The counts in the second column are identical to the rightmost column of Myers’ table. The rightmost column is my own personal Column of Shame, 603 shapes that my program has not had sufficient time to classify. Ideally, over time those numbers will go down as I compute more of the Heesch numbers of these recalcitrant shapes. Who knows—maybe I’ll find a “unicorn” with Heesch number 3 or higher. Fortunately, I can bring ever-greater computational resources to bear in solving this problem. For example, the University of Waterloo recently unveiled the positively massive Graham supercomputer, which I used to compute some of the numbers in this table.
| n | Hole-free non-tilers |
Heesch number 0 |
Heesch number 1 |
Heesch number 2 |
Unclassified |
|---|---|---|---|---|---|
| ≤ 6 | 0 | ||||
| 7 | 3 | 1 | 2 | ||
| 8 | 20 | 6 | 14 | ||
| 9 | 198 | 77 | 120 | 1 | |
| 10 | 1390 | 770 | 620 | ||
| 11 | 9474 | 6029 | 3409 | 26 | 10 |
| 12 | 35488 | 29114 | 6369 | 5 | |
| 13 | 178448 | 152346 | 26048 | 40 | 14 |
| 14 | 696371 | 642259 | 53537 | 26 | 549 |
Note from the future: as of late 2019, this table is out of date. I’ve extended the enumeration to 16-ominoes and found some errors in the numbers above. I’m hoping to write up a new post in early 2020; in the meantime contact me if you need the updated numbers for some crucial purpose.
If you would like to see the set of 98 polyominoes in the table above that have Heesch number 2, or if you’re interested in running your own experiments on them, you can download a simple text file that describes them. I hope the file format is self-explanatory.
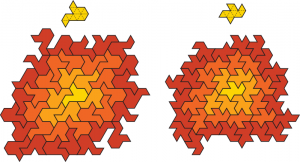
I have also conducted searches over polyiamonds (glued-together equilateral triangles). I didn’t get quite as far, and there were no startling discoveries. But one happy result is that we don’t have to search that far to discover a few new shapes with Heesch number 3. Here are the two examples I’ve found, a 12-iamond and a 10-iamond, with sample 3-coronas.
This same search yielded about 800 polyiamonds with Heesch number 1 and 15 polyiamonds with Heesch number 2. But I don’t trust these relatively old records enough to put them into table form, as I did for polyominoes above; I’d want to re-run the search before I did that.
Closing thoughts
Having started this project, I’m naturally hoping to finish classifying the shapes that I’ve begun working on, particularly those pesky 13- and 14-ominoes. I simply want to know what these shapes’ Heesch numbers are, particularly whether there are any large ones waiting to be discovered.
But as a computer scientist, there’s a much deeper question to consider. When I think about the unknowns I’m trying to find, I must also include the algorithm that’s doing the work. The real research contribution would not be a table of new Heesch numbers to contemplate, but a more efficient technique for computing them. Is that even possible? Can there exist a program for computing a shape’s Heesch number that doesn’t more or less try every possible means of surrounding the shape? In a way, this is one of the central themes of the field of combinatorics: knowing how many objects have a specific property without explicitly constructing them. It’s the difference between counting and enumerating. I don’t need to write down every subset of the integers from 1 to n to tell you that there will be 2n of them—the final count is something we just know. Closer to the topic at hand, Iwan Jensen developed an algorithm for counting polyominoes without enumerating them, allowing him to know how many n-ominoes exist for very large n without ever seeing them. Could an algorithm exist that can determine a shape’s Heesch number without constructing surrounds? If you want a simpler starting point, consider whether there is an efficient algorithm to determine whether a shape has any surround at all, one that avoids explicitly constructing partial surrounds of the shape in every possible way.
I’m not quite sure why I am so drawn to this problem. I suppose that it’s a classic example of recreational mathematics, a path to the discovery of shapes with surprising or exotic properties. The arrangements that emerge are interesting too—not as orderly as a tiling, but still structured somehow. And of course, this path could also lead to profound mathematical insights later, if enough patterns could be found in the data.
More than anything else, though, I can’t help but feel a bit like an astronomer. There’s a vast universe of shapes “out there” waiting to have their properties probed, and the best I can do is slowly sweep my computational telescope across the sky, hoping to stumble upon some exciting new object. As a Mathematical Astronomer, I always crave the next bigger telescope, which will allow me to probe ever deeper into the heavens. My laptop is the equivalent of looking up at the moon through a small telescope in my backyard. When I shift the work over to a supercomputer like Graham, it evokes the image of Ellie Arroway in the movie Contact, pressing a few keys on her laptop and causing a row of radio dishes at the Very Large Array to turn. Here’s hoping that my own personal Wow! signal is out there.


Leave a Reply to Herman Tulleken Cancel reply