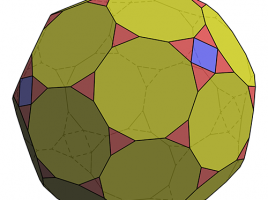
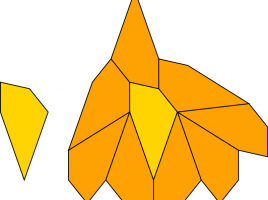
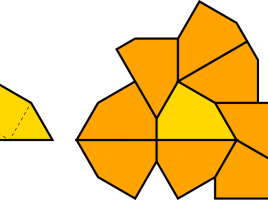
Heesch Numbers of Unmarked Polyforms
After a few years of not writing about the subject here, I’m happy to offer an update on Heesch numbers! If you want to save time, you can skip right to the paper I wrote, or experiment with the associated dataset. Back in 2017, I wrote a series of four …