A Molecular Near Miss!
I’m thrilled to report that I’m a co-author of the article “An ultra-stable gold-coordinated protein cage displaying reversible assembly“, which was recently published in Nature. This work is the result of an exciting collaboration between biochemists, physicists, structural biologists, mathematicians, and others (including yours truly, a computer scientist!), spread over at least five countries on three continents. The project is overseen by Jonathan Heddle from the Małopolska Centre of Biotechnology at Jagiellonian University in Poland.
Now, I do not have sufficient expertise in most of the science behind this work to unpack the whole article here; you might instead read the summary that appeared in Nature‘s “News and Views” section. My contribution relates to a few words that the journal chopped off of the end of the title due to space constraints. The original title read “…reversible assembly and paradoxical geometry“. The phrase “paradoxical geometry” refers to near-miss Johnson solids, a topic that I’ve studied for a long time; the “protein cage” referred to in the title is, from my point of view, a near miss realized at molecular scale (a fact that is mentioned only in passing in the News and Views summary). I helped to explain the geometry of the cage, and to some extent measure just how paradoxical it is. Here I will give a bit of background on this topic, leading up to a geometric view of the cage’s structure.
Near misses
The five Platonic solids, the thirteen Archimedean solids, and the prisms and antiprisms are convex polyhedra with regular polygons as faces. But they’re not the only polyhedra with this property. For example, you can imagine a square-based pyramid that’s just tall enough that its triangular sides are equilateral. In 1966, Norman Johnson identified 92 additional convex polyhedra with regular faces, starting with the square-based pyramid; today these are known as the Johnson solids. They’re a motley crew of geometric oddities, which look as if they were assembled out of leftover parts from the Archimedeans.
In 2001, George Hart and I published a paper about polyhedra in which we included a brief mention of “near misses”: convex polyhedra with faces that are almost—but not quite—regular. We did not attempt to define near misses rigorously, merely saying that the angles were close enough that you could assemble a model from cut-out regular polygons “without noticing the discrepancy”. The paper offered these three examples:

The second and third polyhedra are easily exposed as Johnson solid impostors, by identifying vertices that could not exist in a Johnson solid. For example, the second polyhedron has a vertex surrounded by two hexagons and two triangles. A regular hexagon has an interior angle of 120°, and an equilateral triangle has an interior angle of 60°. So, if those faces were all regular, the angles around the vertex would be 60° + 60° + 120° + 120° = 360°. But that’s impossible! When you pack that much angle around a vertex, you force the faces there to lie flat, contradicting our assumption that this polyhedron is convex. The polyhedron on the left is not so easily dismissed. You need to grind through some trigonometry to prove that if the enneagons (9-sided polygons) and squares are regular, then the triangular faces are slightly isosceles and not really equilateral (I get an angle of about 63.1° at the triangle vertex nestled between two enneagons).
I’ve written about near misses elsewhere, including a 2016 post about a new one I had constructed. In 2017, Evelyn Lamb wrote a wonderful article about the more general phenomenon of near misses in mathematics, leading off with near-miss Johnson solids. She also had the good fortune to interview Norman Johnson, who noted that he stumbled on near misses while enumerating his solids, but cared about them only to the extent that he had to eliminate them from his list. Sadly, Johnson passed away shortly after the article was published.
A hendecagonal near miss
Around the time that we wrote that 2001 paper, I found another interesting near miss, one that didn’t fit with the techniques in the paper. To construct it, start with the pentagonal icositetrahedron (PI), the dual of the more familiar (and Archimedean) snub cube. This solid is made from 24 identical shield-shape pentagonal faces:

Pentagonal icositetrahedron. Image by Maxim Razin.
Let’s focus on a single shield, as in the shape on the left below:
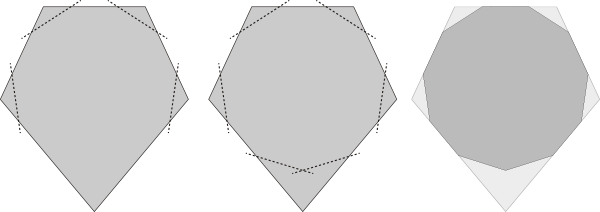
We can imagine slicing through each of the four upper corners of the shield, as suggested by the four dashed lines. If we do this correctly, the corners are truncated to create new edges that have the same length as the leftover bits of the original shape. The pointy bottom of the shield still sticks out, but by coincidence we can just about fit two more short edges into the point, as shown in the middle. The right drawing shows that these lines define a shape that bears an uncanny resemblance to a regular hendecagon (i.e., a regular 11-sided polygon).
Looked at another way, if we take a perfectly regular hendecagon and fit it by eye to the shield, we can achieve an amazingly good fit. In the diagram below, I’ve lined up the midpoints of the top edges of a shield and a regular hendecagon, and manually scaled the latter until it straddles the edges of the former. The close-up shows just how tight the fit is. You can just barely see the hendecagonal edge tilted relative to the shield edge.

As a final demonstration of the closeness of the fit, let’s compare angles in the shield and the hendecagon:
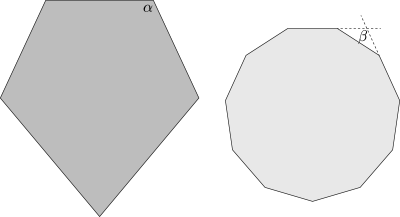
The angle α on the left is a property of the PI, and measures around 114.8°. The angle β on the right is exactly 180°⨉(7/11), or around… 114.5°. Again, an amazing coincidence, one that makes it possible to inscribe the hendecagon almost perfectly within the shield.
To complete the construction of a near miss, we can simply glue together regular hendecagons in the same pattern as the shields in the PI. The holes around the tops of shields can easily be filled with equilateral triangles, and the holes around the pointy corners of shields can be filled with clusters of four triangles around a square. Here’s the result:
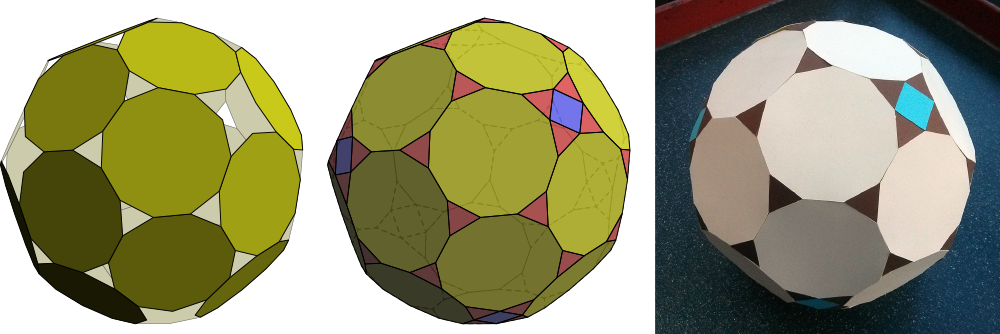
The paper model on the right is actually easiest to construct, because you can let the laws of physics absorb and distribute the mathematical error inherent in the construction. To build a computer model, you must make explicit decisions about where that error should go. For example, the faces could be made slightly irregular, or slightly non-planar.
Again, I have no rigorous test for near-miss-ness that I could apply to this solid. But intuitively, the miss is very near indeed, and the paper model can easily be constructed without noticing the error.
As an aside, my goal at the time was to create interesting tilings of the sphere to serve as a scaffolding for drawing spherical Islamic geometric patterns. I eventually created a few 3D designs based on the techniques in the paper, and on the hendecagonal near miss. I then turned these models into 3D printed sculptures.

Two 3D-printed spherical Islamic geometric patterns. The one on the left has icosahedral symmetry and features large 9- and 10-pointed stars; the one on the right is based on the hendecagonal near miss and features large 11-pointed stars.
However, I didn’t have much else to say on the mathematics of near misses, so I put the shape on a short web page and left it at that.
The TRAP Cage
Fast forward to late 2013. A team of biochemists had been working with a custom-engineered protein ring called TRAP, which they knew had 11-fold rotational symmetry. They observed that under suitable encouragement from gold nanoparticles, a set of TRAP rings would assemble into a round solid form, which they called a TRAP Cage. But the structure of this cage was something of a mystery, because they didn’t know of a simple geometric form made from pieces with 11-fold symmetry. I assume they searched the web for polyhedra with hendecagonal faces, because they eventually found me by chance. And sure enough, it looked like the TRAP rings in their cage were arranged like the hendecagons in my near miss!
I joined the collaboration, with the aim of building a computational model of the TRAP Cage, from which we could measure the likelihood that the cage could hold itself together based on the distribution of error in the model.
The TRAP Cage is a bit more flexible than the near miss. First, it is constructed purely from TRAP rings, so we don’t have to worry about fitting squares and triangles into the model. Second, the rings aren’t actually attached directly to each other as they would be in a polyhedron; instead, the ring has 11 tiny arms that stick out, and arms from neighbouring rings grab on to gold atoms to hold the structure together. This extra flexibility means that we can likely construct a model cage with even lower error than the original near miss.
I tested this hypothesis using numerical optimization, searching for a symmetric arrangement of TRAP rings for which the gold bonds would have the correct lengths predicted by chemical considerations. The goal of the optimization was to minimize the worst error in bond length, while also trying to keep the arrangement of TRAP rings as round as possible.
This optimization was easily able to find virtual cages where the bond lengths between neighbouring rings never deviated by more than one part in a billion from their ideal lengths. That’s an astonishing degree of nearness for a near miss. I’m not a physicist, so I can’t say exactly how near, but allow me to speculate. I’ve got to assume that this deviation is well within the chemical tolerances for atomic bonds, meaning that the TRAP Cage would hold together without ever running afoul of its own mathematical impossibility. Going further, I note that the ideal bond length was given to me with just two significant digits, suggesting that an error of one part in a billion is much smaller than our uncertainty in measuring the “true” bond length in the first place. In other words, we may as well round the error to zero in the messy real world.
The TRAP Cage is, then, a real-world near miss at molecular scale: you could build it out of regular microscopic pieces without, as I said earlier, “noticing the discrepancy”.
Conclusion
The article appeared in the May 16th issue of Nature. Even if you’re not a subscriber, they have provided a link that will allow you to read the full article. I tried to use my meagre 3D modelling skills to create a flashy image for the issue’s cover, but it didn’t pass muster. Of course, my blog is the perfect place to display the image.
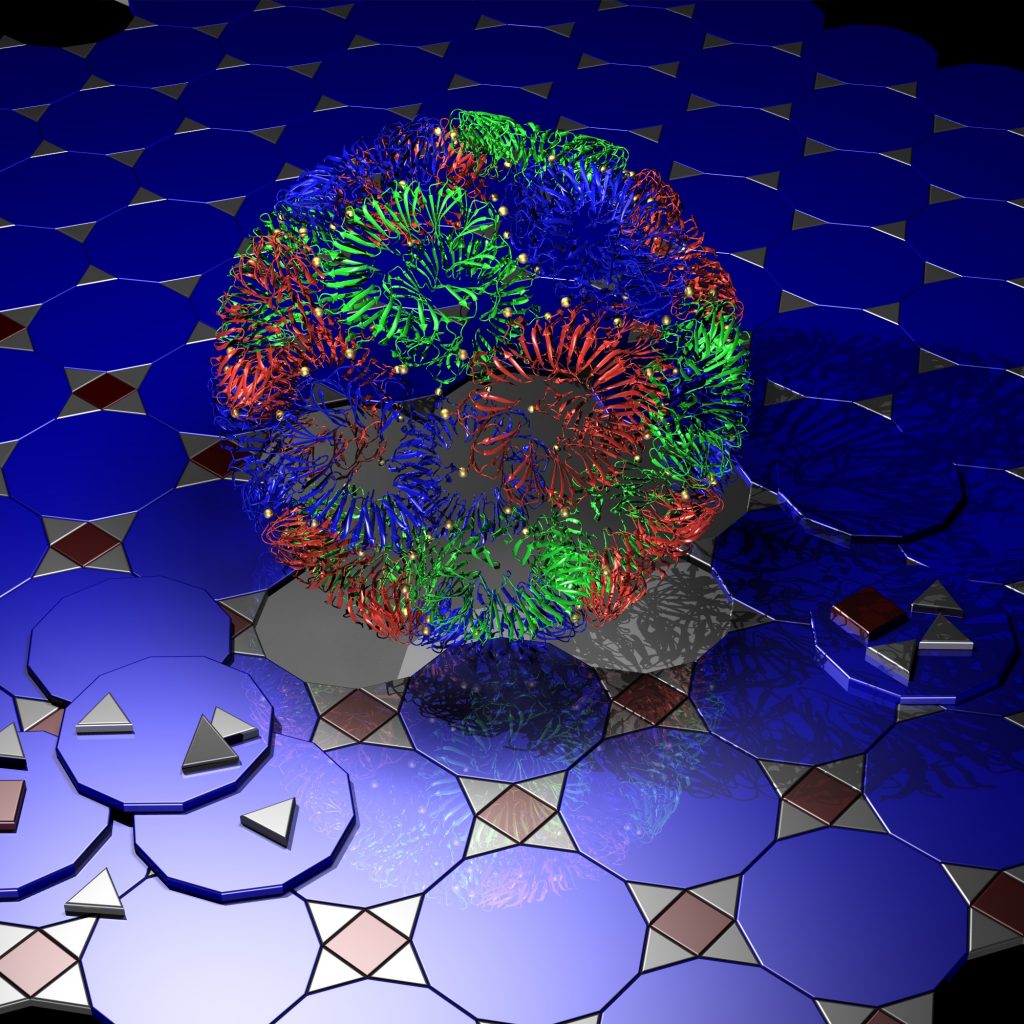
A glamour shot of the TRAP Cage. A visualization of the biological structure of the cage (with gold atoms highlighted) sits on a field of two different Euclidean tilings, suggestive of the structure of the original near miss.
I’m incredibly excited to see this curious corner of geometry find a real-world application. Perhaps this discovery will motivate me or others to establish a more rigorous theory of near misses. Indeed, Agnieszka Kowalczyk, a mathematics PhD student at Jagiellonian University, together with Bernard Piette from Durham University, are already researching other cage structures with “paradoxical geometry” and have found numerous examples (aided by the fact that these cages don’t need to be fully watertight like polyhedra). They force their polygons to join edge-to-edge but permit them to deform slightly away from regularity, and then work on measuring and minimizing that deformation. They’ll be presenting some of their initial findings at this year’s Bridges conference in Linz. I’m looking forward to seeing what else we can do with this work.
Leave a Reply to Craig Kaplan Cancel reply