Lecture notes

After completing each module of the course, I typically post an extended set of lecture notes here, which summarize the main points of the lecture and provide pointers to any papers discussed.

Lecture 1: Introduction

The first half of this lecture presented the basic logistics of the course, which is already well covered by the syllabus page.

The second half presented a tiny slice of the history of relationships between computer graphics and art, and tried to motivate the content to be discussed in the rest of the course.

I began with what is now a cherished view in the NPR community. Photorealism is limited in expressive range, because it really has just one goal. Non-photorealistic rendering generalizes computer graphics to a broad range of styles, levels of abstraction, and techniques, and is therefore capable of more effective communication tailored to content. In this respect, photorealism may be regarded as just one possible style under the larger umbrella of “stylized rendering” or “expressive rendering”. Many of these thoughts are lifted from the introductory slides in Aaron Hertzmann’s 2007 NPR course, some of which are themselves adapted from earlier lectures by David Salesin and Pat Hanrahan.
I held up Manfred Mohr and Harold Cohen as early examples of computer artists (though Cohen continues to develop his AARON software to this day). The history of computer art now spans more than five decades, long enough to have developed into a field that can be studied and analyzed in isolation. If you are interested in art history and critical theory, it may be worth taking a look at Taylor’s recent book When the Machine Made Art: the Troubled History of Computer Art. (I learned of this book because the journal I edit recently published a review of it.)
The development of NPR as a research area within computer graphics is generally traced back to two influential early papers: Hairy Brushes (Strassmann 1986) and Paint By Numbers: Abstract Image Representation (Haeberli 1990). The former is a good archetype for procedural systems that simulate natural media; the latter can represent algorithms for image abstraction.
I mentioned the origin of the term “non-photorealistic rendering”, generally taken to have occurred in the introduction to the 1994 paper Computer-Generated Pen-and-Ink Illustration by Winkenbach and Salesin. This term has never been particularly well regarded (as Ulam famously said in a different context, “Using a term like nonlinear science is like referring to the bulk of zoology as the study of non-elephant animals”); nevertheless, it has become entrenched.
I finished with a very brief mention of the history of ornamental design and patterns in computer graphics research, in order to foreshadow the second half of the course. The earliest paper I’m aware of is from the second SIGGRAPH conference in 1975: The computer/plotter and the 17 ornamental design types by Alexander. That paper used a plotter to generate patterns in each of the 17 wallpaper groups (discrete planar symmetry groups with periodic symmetry). Not long after, Dunham et al. extended these ideas to create what I believe are the first computer-generated images of hyperbolic geometry. See for example the paper Creating repeating hyperbolic patterns, from SIGGRAPH 1981.

Lecture 2: Halftoning

Halftoning refers to any process that approximates the appearance of continuous tone (darkness) using only marks of one colour on a contrasting background (usually, black on white). The term halftoning was first used in reference to processes that would allow black-and-white photographs to reproduced in large quantities in print, as was first done in newspapers in the late 1800s. Of course, the idea of approximating continuous tone goes back much further, to the earliest uses of hatching and stippling in art. These techniques became further cemented in art with the proliferation of printmaking methods like woodcuts and copperplate engraving.

Practical digital halftoning began to appear in the 1970s, as it became feasible to represent a raster image in a computer’s memory, to run an algorithm to approximate with black and white pixels, and to emit those pixels to some kind of pixel-addressable output device. The definitive book on digital halftoning, which goes into considerable detail on these original algorithms, is undoubtedly Ulichney’s book Digital Halftoning. We can see halftoning algorithms as spanning a range of abstraction from photorealistic to non-photorealistic, with some of the NPR-related ideas captured in the older textbook by Strothotte and Schlechtweg. More recently, Deussen and Isenberg contributed a chapter to the book Image and Video-Based Artistic Stylisation about halftoning and stippling, which is even more tuned to the material in this module.

Here are the specific halftoning ideas and algorithms I covered in this module:

I started with simple pixel-based computations in which a decision can be made about every pixel in a greyscale image independently. The simplest decision I can think of in this regard is called thresholding: if a pixel is brighter than middle grey, round it to white, otherwise round it to black. Unsurprisingly, thresholding tends to do a pretty poor job all around. In some limited situations, we can get more mileage out of adaptive thresholding, in which a pixel’s brightness is compared not to middle grey, but to the average (or some other weighted sum) of the pixels in its neighbourhood.
A single pixel cannot communicate tone well on its own, but an 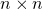$n\times n$ block of pixels can represent a range of 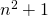$n^2+1$ grey levels, one for every number of black pixels in the block. If we start with an image of dimensions 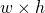$w\times h$ , it’s clear then that we can quantize it to 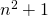$n^2+1$ tones using an image of dimensions 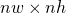$nw\times nh$ . Of course, we may not have that much resolution to spare…
Let us assume further that the aforementioned 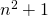$n^2+1$ blocks are “cumulative”, in that each successive grey level is derived from the one before it by adding a single black pixel. We can summarize this sequence of blocks via a single 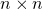$n\times n$ matrix whose entries use each of the numbers 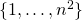$\{1,\ldots,n^2\}$ once. Slightly less obvious is the fact that we can turn this matrix into a matrix of “local thresholds” by dividing every element by 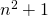$n^2+1$ . We can then tile a source image by copies of this matrix and apply the tiling as a grid of thresholds. To a first approximation, this approach lets us get the halftoning behaviour of the previous one without blowing up the resolution by a factor of 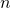$n$ . This algorithm is called ordered dithering; typically, it uses a beautiful, recursively defined set of 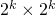$2^k\times 2^k$ dither matrices called the Bayer matrices.
In dithering, every local thresholding decision incurs some amount of error. The dithering algorithms above are limited, in that there’s no mechanism for balancing or distributing this error—every pixel simply discards the “ink” (or lack thereof) that it wasn’t able to account for. This deficiency is the motivation for error-diffusion dithering, in which we shift this residual error to unprocessed pixels instead of simply “leaving it on the table”. The classic example of an algorithm in this class is Floyd-Steinberg dithering: we march through an image in row-major order, using a simple matrix of weights to distribute error to unprocessed pixels beside and below the current one. Floyd-Steinberg works pretty well, though there’s lots of room for improvement, as in this 2001 SIGGRAPH paper by Ostromoukhov. Even the question of how best to evaluate these algorithms is far from solved.
Dithering can only get you so far when the goal is non-photorealistic rendering—it’s hard to get a lot of control over the patterns introduced by the halftoning process. A more useful starting point is digital screening. Conceptually, screening behaves like ordered dithering: a greyscale screen is placed on top of an image. The screen acts as a spatially varying threshold for pixels in the image. This process gets interesting because we can manipulate the “shape” of the screen to produce characteristic patterns that interact with the halftoned image. I discuss two graphics papers that take their inspiration from screening: Digital Facial Engraving (Ostromoukhov, SIGGRAPH 1999), and Artistic Screening (Ostromoukhov and Hersch, SIGGRAPH 1995).