Aperiodic Monotiles

Now that I’ve written up posts about some of the smaller projects that have occupied my time over the past 18 months or so, it’s time to talk about the Big One, the real reason I came back to this blog in the first place. I don’t want to re-tell the whole (long) story, and I don’t want to give a self-contained account of all the math or computation behind this work. So consider this post to be a quick introduction to the events of the past year, and a few of my personal reflections on the experience. At the end, I’ll include links to other resources where you can learn more.

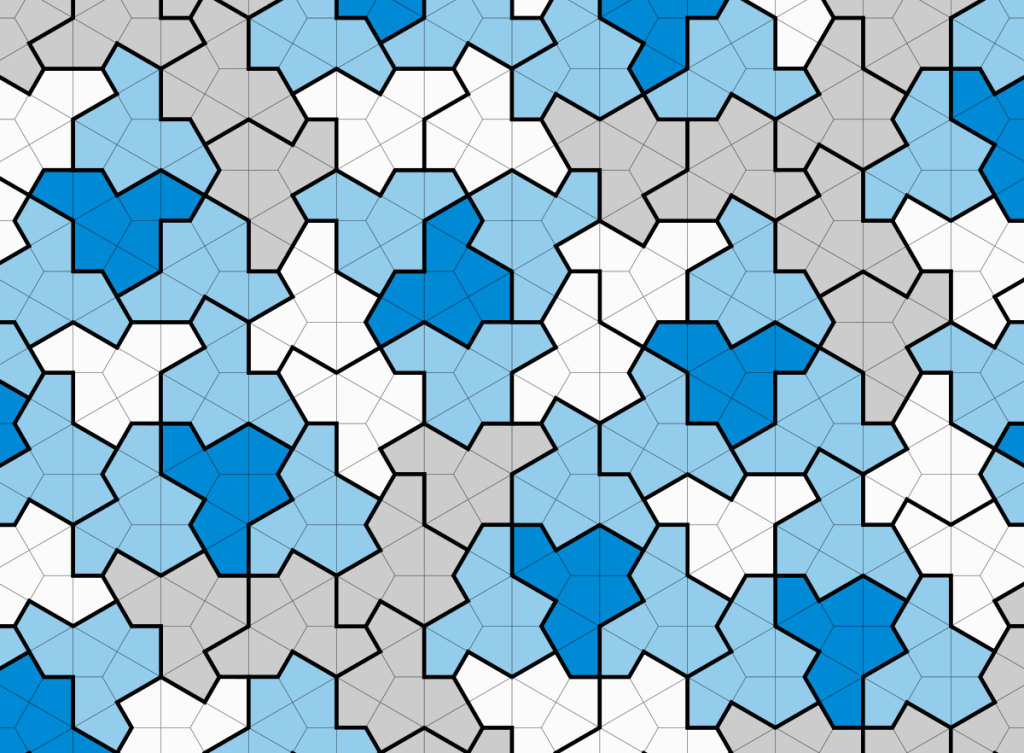
In November of 2022, Dave Smith emailed me out of the blue. Dave was a casual acquaintance from the world of tilings. I knew him from his blog (which he has since moved) and his occasional posts on a mailing list to which we both belong. As far as I can tell, outside of the mailing list we had exchanged about two or three emails with one another in previous years. He was renewing contact because he had encountered a real puzzle involving a simple shape (the one shown with thick outlines above).

This is the moment in the science fiction movie where the scientist first discovers The Anomaly. A cell in a microscope slide that doesn’t look like its neighbours. A new dot of light in a telescope image. I inevitably think of Jodie Foster’s character Ellie Arroway in the movie Contact, upon first hearing the message from Vega: her eyes go wide and she utters the modern equivalent of “Eureka”, namely “Holy shit”. This shape was Dave’s Anomaly. He was trying to determine whether or not it could tile the plane, but it was refusing to behave, and Dave couldn’t obtain a clear answer either way.

Through a combination of hand tinkering and computer analysis (made possible because of additions to my tiling code by undergraduate researcher Ava Pun), Dave and I quickly determined that The Anomaly was real. This shape wasn’t conforming to our usual expectations for tilings. In fact, it looked like it could very well be an aperiodic monotile, a solution to the decades-old unsolved “einstein problem”. Such a shape would tile the plane, but never in a regular, grid-like fashion. Aperiodic tilings have been documented since the 1960s, but despite considerable effort nobody had been able to find a way to achieve aperiodicity with a single shape; the smallest sets we knew of used two shapes, like Penrose’s kite and dart. And of course, nobody had been able to prove that an aperiodic monotile was impossible either.

Dave and I continued to play around together for the rest of 2022. We managed to unravel a few of the secrets of this shape, which we were now starting to call “the hat”. In particular, I found a couple of sets of substitution rules by which we could construct arbitrarily large patches of hats. In the new year, we followed through on another movie trope: it was time to assemble The Team, a group of eccentric misfits with complementary skills who could crack the case together (in a movie, this would be accomplished via a montage, of course). We reached out to mathematicians Chaim Goodman-Strauss and Joseph Myers. Dave and I knew both of them from the same mailing list. I had interacted with Chaim at past conferences, both research-oriented and recreational. I had been familiar with Joseph’s work on polyform tilings for decades, and had even contributed a little to it around 2006 with my former Master’s student Paul Church.

Of the four of us, Joseph became the mathematical MVP. In record time he completed a rigorous proof that Dave’s hat was indeed an aperiodic monotile. That would already have been enough for a significant paper, but Joseph quickly doubled down with additional profound insights. He figured out that a second anomalous shape Dave had discovered back in December, the “turtle”, was also an aperiodic monotile. That then led to the discovery that the hat and turtle were merely two points on a continuum of shapes, all of which tiled in the same way. In a final flourish, Joseph used the existence of that continuum to drive a second, wholly new proof of aperiodicity, something that none of us could have expected at the outset.

We put the paper online in March and were delighted, flattered, and overwhelmed by the enthusiastic response it received from mathematicians, hobbyists, and the media. The paper generated a lot of activity. Artists got to work making things based on the tiles. Mathematicians studied the paper and debated the ideas it contained.

To our relief, nobody came forward to point out a fatal flaw, but one criticism was frequently aired: the use of reflections. Every tiling by the hat needed both unreflected and reflected hats (or, if you prefer, left-handed and right-handed hats, or hats and anti-hats, etc.). In fact, in any tiling by hats, about 1/7 of the tiles (more precisely, 1 in 6.8541…, the fourth power of the golden ratio) must be reflected relative to the rest. Some people argued, perhaps motivated by the manufacture of physical tiles, that a shape and its reflection ought not be considered as “the same”. While I disagree from a mathematical standpoint, these criticisms suggested a worthy follow-up question: could a shape exist that tiled aperiodically without ever needing to be flipped over? Simply put, we had no idea.

Six days later, Dave spotted an Anomaly within The Anomaly! Inspired by some of Yoshi Araki’s drawings, Dave began to experiment further with the shape denoted Tile(1, 1) in the image above (for which Dave Keenan and Douglas Blumeyer suggested the excellent name “hurtle”, given that it’s halfway between a hat and a turtle). That shape is unusual within Joseph’s continuum: all its edges have the same length (if you regard the long edge as two short ones), allowing it to fit together with copies of itself more freely, and in particular to tile the plane periodically. But eagle-eyed Dave noticed that if he forbade reflections, it started behaving strangely again. We reassembled The Team and in short order we discovered that, sure enough, this shape tiles aperiodically if you restrict yourself to translations and rotations only. Better yet, that means that just about any modification to its edges yields a new shape that Dave called a “Spectre”, which is unconditionally a “one-handed aperiodic monotile”: every tiling admitted by a Spectre must be non-periodic, and must use tiles of a single handedness only. Spectres laid to rest any doubts that might have lingered over the hat’s use of reflections. We posted a follow-up paper at the end of May and it too was warmly received.

The entire process of discovery and research was utterly surreal. The hat is a comically boring shape that had been catalogued by others many times in the past. But as a solution to the einstein problem it was hiding in plain sight: past work had never considered its tiling properties. (Perhaps it’s better to say that it was just one more nondescript shape in an overwhelming sea of similar-looking candidates, each of which would have to be considered in turn using brute-force computation.) The four of us had never worked together before, and by the time we started collaborating I was the only active researcher (Chaim had just moved to the Museum of Mathematics in New York). And yet, we managed to produce a convincing solution to a longstanding open problem in record time, with all communication restricted to a single epic email thread. I’m sure that in part, our success is due to the decades we had collectively put into thinking about the einstein problem. Here I’m reminded of the Map with no Names in Indiana Jones and the Last Crusade: we knew the route we’d have to take to a proof, if only we knew what shape to begin with. The hat was our Iskanderun.

Luck played a role throughout the process too. I was lucky that Dave chose to reach out to me, and that I had the bandwidth to dive in. We were lucky to recruit Chaim and Joseph to work with us. At a deeper level, we were lucky that the math was “on our side”, a tailwind pushing us towards a solution. The hat need not have succumbed to the kinds of analyses used previously to establish the aperiodicity of other sets of tiles—in truth, we just don’t know enough about the limits of aperiodicity to be sure of what forms it might take. Fortunately, our usual tools were nearly a perfect fit. And we were lucky beyond all measure that Dave plucked the miraculous Spectres from Joseph’s continuum. Although our second paper makes it clear that Spectres have the properties we want them to have, to this day I cannot see any good reason whatsoever why one-handed aperiodic monotiles should be connected to the hat. It’s a good reminder that while we gathered a couple of new facts about aperiodicity, there’s still so much we don’t understand.

I was on sabbatical during 2023. I submitted paperwork to my university in the summer of 2022 suggesting I had a few ideas for what I wanted to do during the year; looking back, I accomplished almost nothing on that list. Indeed, one of my plans had been to start working on a book about unsolved problems in tiling theory, a plan that we’ve clearly undermined by solving one of the problems I wanted to write about! instead, it was a whirlwind year of research, interviews, invited talks, and a seeming reinvigoration of interest in the mathematics of tilings. Combined with lots of fascinating research with graduate students on topics that had nothing to do with this one, it was about as fulfilling a year as I can imagine having, career-wise. Zooming out, it’s plausible-to-probable that this is the most significant result I will ever achieve as a researcher. While it’s bittersweet to contemplate that possibility as it’s unfolding, I won’t have any regrets if it pans out. Perhaps my equanimity is a symptom of middle age, though of course I’ll keep striving to top myself.

If you had asked me before November 2022 about my favourite open problems in mathematics, I would certainly have mentioned the einstein problem, among others. This problem was dear to me for a few reasons. First, it seemed like a remarkably profound question about geometry, whose answer was a complete mystery. Second, unlike other famous open problems (like, say, the Riemann Hypothesis or P vs. NP), there wasn’t an obvious side to root for: I could easily have believed in either the existence or non-existence of an aperiodic monotile. Third, unlike other famous open problems, my eclectic mathematical and computational background gave me some hope of pushing the frontier of knowledge in this area. Still, I don’t think I could have conceived of the possibility of contributing directly to the solution of an open problem of this magnitude. I would have been content just to learn that a solution had been found; to have been part of it feels like an unfathomably rare gift from the universe. Thanks, universe.

Additional resources

As I said above, I can’t possibly capture either the necessary mathematical background or the history of our discovery in a single blog post. The superficial introduction above is already more than long enough! Instead, I’d like to offer a few links to pieces by ourselves and others where you can learn more. Even this list is necessarily incomplete, and I apologize in advance to anybody I’ve left out—I admire and appreciate the effort I’ve seen journalists, bloggers, and others put into interpreting our work for a general audience. I’m also focusing on general overviews of aperiodic tilings and our work, and leaving out the amazing follow-up research by others that has already happened and is starting to appear online.

Papers, code, images, animations

The homepage for the hat, including a link to the arXiv preprint, interactive browser-based apps for playing with tiles, galleries of images and animations, downloadable code for verifying some of the claims in the paper, and a few additional links.
The homepage for Spectres, with analogous materials for our second paper on one-sided aperiodic monotiles.

Writings and videos by the authors

My article, “Inside Mathematicians’ Search for the Mysterious ‘Einstein Tile’“, which appeared in the January 2024 issue of Scientific American. (Behind a paywall, sorry)
A blog post by Dave on the discovery of the hat, which contains a lot of fun work-in-progress images. He also wrote a second blog post about the discovery of Spectres.
The authors participated in two virtual discussions for the Museum of Mathematics back in March. The first video includes more formal presentations by me and Chaim; the second is a less formal “meet the authors” event with lots of questions and discussion.
A video from Hatfest, an event held at Oxford in July. The first half of the video is a gentle introduction by Chaim to the topic and our work. The second half is a more wide-ranging panel discussion with me, Chaim, Marjorie Senechal and Sir Roger Penrose, moderated by Henna Koivusalo.
My talk from Hatfest, which tells the story of our discovery in a publicly accessible way.

Other writings

Jim Propp’s essay “Seekers of the One-Stone” is an excellent all-around introduction to the topic and our tiles, and includes some of the mathematical details.
Siobhan Roberts wrote a few extensive articles about our discoveries for the New York Times. See “Elusive ‘Einstein’ Solves a Longstanding Math Problem” and “With a New, Improved ‘Einstein,’ Puzzlers Settle a Math Problem“. (Also paywalled)
Erica Klarreich wrote an accessible article, “Hobbyist Finds Math’s Elusive ‘Einstein’ Tile“, for Quanta Magazine. (The photo of Dave in that article might have been the first time I saw what he looked like!) Soon after, Patrick Honner published a nice introduction to aperiodicity with his Quanta article “Math Patterns That Go On Forever but Never Repeat“. David Richeson also mentioned our work in his overview “A Brief History of Tricky Mathematical Tiling“.

Other things

The Grimm Network has a nice gallery of photos from Hatfest.
The Museum of Mathematics and the UK Mathematics Trust held a wonderful worldwide contest to create art or design objects based on aperiodic monotiles. They published an amazing gallery of the winners and finalists.

Bill lipner says:

January 9, 2024 at 5:20 am

Are tiles ever considered in 3 dimensions?

Craig Kaplan says:

January 9, 2024 at 9:51 am

Good question! Yes, they’re absolutely considered. But honestly we don’t know all that much about aperiodic monotiles in 3D. There’s a single well known example called the Schmitt-Conway-Danzer Biprism that acts as a kind of 3D aperiodic monotile. But there are good reasons to complain that it’s not quite what we’re looking for. It seems quite reasonable to assume that something like the hat exists in 3D, but as in 2D it’s hard to find (and probably harder to reason about, even once you’ve found it).