
Currently browsing author
Craig Kaplan


Swirled Series: The Result

Swirled Series
The Metaphysics of Speed Limits
(define (speeding-fine speed) (cond [(< speed 100) 0] [(and (>= speed 100) (< speed 120)) (* 3.00 (- speed 100))] [(and (>= speed 120) (< speed 130)) (* 4.50 (- speed 100))] [(and (>= speed 130) (< speed 150)) (* 7.00 (- speed 100))] [(>= speed 150) (* 9.75 (- …

Mathematical Animated GIFs
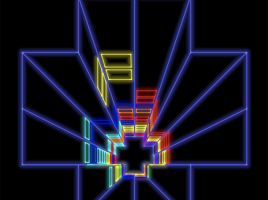
Temptris

Andromeda Reimagined

Escher-like Spiral Tilings
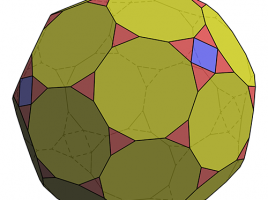
A Molecular Near Miss!

Hexagonal Cross Stitch
At least year’s Bridges Conference in Stockholm, I attended a short presentation by Susan Goldstine about “self-diagramming lace”. As motivation for the new work she was presenting, Susan referenced her paper from the year before on what she calls “symmetry samplers”. Samplers are an old tradition in fibre arts. A …