Heesch Numbers of Unmarked Polyforms

May 23, 2021

After a few years of not writing about the subject here, I’m happy to offer an update on Heesch numbers! If you want to save time, you can skip right to the paper I wrote, or experiment with the associated dataset.

Back in 2017, I wrote a series of four posts about Heesch numbers. If you like, you can get acquainted with the subject by having a look at the first post in the series. Briefly, a shape’s Heesch number is the number of times you can surround the shape by layers of copies of itself without copies overlapping or enclosing holes. In an ill-timed coincidence, these layers are usually known as “coronas”, a usage that predates COVID by many years.

Shapes with finite Heesch numbers live on the edge between order and chaos. Their boundaries are well-behaved enough to permit one or more coronas, but not so nice that they tile the plane out to infinity. We don’t know a lot about how to find shapes with interesting Heesch numbers, or even what Heesch numbers are possible. Until last year, I would have told you that the longstanding all-time record was Casey Mann’s shape with Heesch number 5. But I’m delighted to report that earlier this year, Bojan Bašić revealed a new shape with Heesch number 6! How high can these numbers go?

One of the main topics I explored in 2017 was Heesch numbers for families of simple shapes. I focused mostly on polyominoes (shapes made by gluing squares together), though I also wrote briefly about polyiamonds (made from equilateral triangles). Given a polyform known not to tile, at the time I computed a shape’s Heesch number using a brute-force search with backtracking. Such an algorithm is a bit like exploring a maze: every time you come to a branch, you try the first path you see. If that choice eventually allows you to reach the exit, great! But if you end up in a dead end, you back up to that branch and try the second path instead, and so on. If you do this consistently everywhere, remembering your choices at branches, you eventually find the exit or discover that no path leads to it. Translating this algorithm to surrounding shapes, every edge of the shape is a fork in the road, and you can choose any legal way to attach a new neighbouring shape to cover that edge. Any given choice might limit future options and lead to a dead end, in which case you have to choose a different neighbour placement. Eventually you either find a surround or discover that there isn’t one. To compute a shape’s Heesch number, you have to check if any surround can itself be surrounded, and so on for each successive corona.

That’s a painfully expensive process! It’s easy to get stuck in a kind of backtracking hell. There could be a funny wiggle far out along the shape’s boundary that always prevents the shape from being surrounded, but you might need to explore a vast garden of forking paths that all lead to that dead end. The pain is further compounded when exploring higher coronas: proving that a shape has Heesch number 1 involves generating all possible surrounds of it, just to establish that none of them can be surrounded by a second corona. A better algorithm would teleport from point to point around the shape’s boundary, finding features of its boundary that limit how coronas can form. It’s a bit like cordoning off some of the branches in a maze so you know never to explore them. But it’s quite difficult to know where to look for these features, and that still doesn’t help with higher coronas.

And so, my 2017 enumeration has serious problems. I could compute Heesch numbers only for small shapes, and even then computation time varied wildly, from a fraction of a second to weeks or longer. Some computations never produced an answer, forcing me to leave some polyominoes unclassified. And my code had other bugs, causing it to report the wrong Heesch number for some shapes. Yuck.

Computing Heesch numbers with a SAT solver

All that changed in 2019. In a thread on Facebook, Bram Cohen suggested that a SAT Solver could be used to compute Heesch numbers in a way that would likely outperform any hand-tuned algorithm. A SAT Solver is a tool that takes a Boolean formula as input (a bunch of variables, combined together with AND, OR, and NOT operations), and tells you whether there’s any way of choosing true and false values for the variables so that the whole formula comes out true. Bram’s idea was that you could translate the question “does this shape have Heesch number at least n?” into a Boolean formula whose variables represent all possible locations for copies of the shape, and let the SAT Solver grind through these variables, shaking out a subset that defined a configuration of legal coronas.

A SAT Solver isn’t a silver bullet: in the worst case, it can still get stuck in backtracking hell. But these tools are highly optimized, and are really, really good at jumping around the input problem, finding ways to limit the number of branches to explore. And that’s where the SAT Solver will win here. Any heuristics I could implement would be motivated by (and limited by!) a geometric interpretation of the problem. The SAT Solver doesn’t care about geometry: all it knows about is Boolean variables and how to avoid unnecessary work. I love the idea some problems can be solved more easily by being dumber, by thinking less about the intricacies of the problem domain. It reminds me of counterintuitive advice from math contests like the Putnam: sometimes, the best strategy for solving a problem is to solve a harder, more general problem instead. Quanta Magazine has a good article about using a SAT Solver in the context of a different mathematical problem.

Bram’s suggestion was spot-on. He offered a first version of the translation from geometry into Boolean logic, which we then refined by email. (I have since learned that Bram often swoops in, drops a brilliant idea into someone’s lap, and then rides off into the sunset.) The SAT Solver I used, CryptoMiniSat, has no trouble chewing through the computation of Heesch numbers of polyominoes. Its performance is extremely reliable too: on average it requires about 0.15 seconds per shape, and never more than about a minute for shapes with high Heesch numbers, completely avoiding the worst of backtracking hell. And a SAT-based approach generalizes easily to polyiamonds and polyhexes (made from hexagons) too! So, since 2019 I was able to correct errors in my previous enumeration, do away with all unclassified shapes, and extend the enumeration to higher polyominoes, polyiamonds, and polyhexes. As of this writing, I’ve computed Heesch numbers for all polyforms up to 19-ominoes, 17-hexes, and 24-iamonds.

If you’re interested in all of the technical details, I’ve written a paper on this search, which is available on arxiv.org. I’m also making a dataset available containing a few thousand polyforms and their Heesch numbers, as both text descriptions and drawings showing coronas. Below, I summarize a few of the main results.

The data

Of course, I have to start with a new table showing Heesch numbers of polyominoes:

Heesch numbers of polyominoes, no holes in the outermost corona

n	non-tilers	H = 0	H = 1	H = 2	H = 3	Drawings
7	3	1	2			0-up
8	20	6	14			0-up
9	198	75	122	1		0-up
10	1390	747	642	1		0-up
11	9474	5807	3628	39		2-up
12	35488	28572	6906	10		2-up
13	178448	149687	28694	67		2-up
14	696371	635951	60362	58		2-up
15	2721544	2598257	123262	25		2-up
16	10683110	10397466	285578	66		2-up
17	41334494	40695200	639162	130	2	2-up
18	155723774	154744331	979375	68		2-up
19	596182769	593856697	2325874	198		2-up

What a difference! Whereas before I couldn’t even deal with all 700000 14-ominoes, here I’ve handled 1000 times as many shapes. The search even turned up the two smallest polyominoes with Heesch number 3, when n = 17. In the paper I offer a second table, giving alternate Heesch numbers when holes are permitted in the outermost corona. Click on the link in the rightmost column for a PDF from the dataset containing either all non-tilers (0-up) or shapes with Heesch number 2 and higher (2-up).

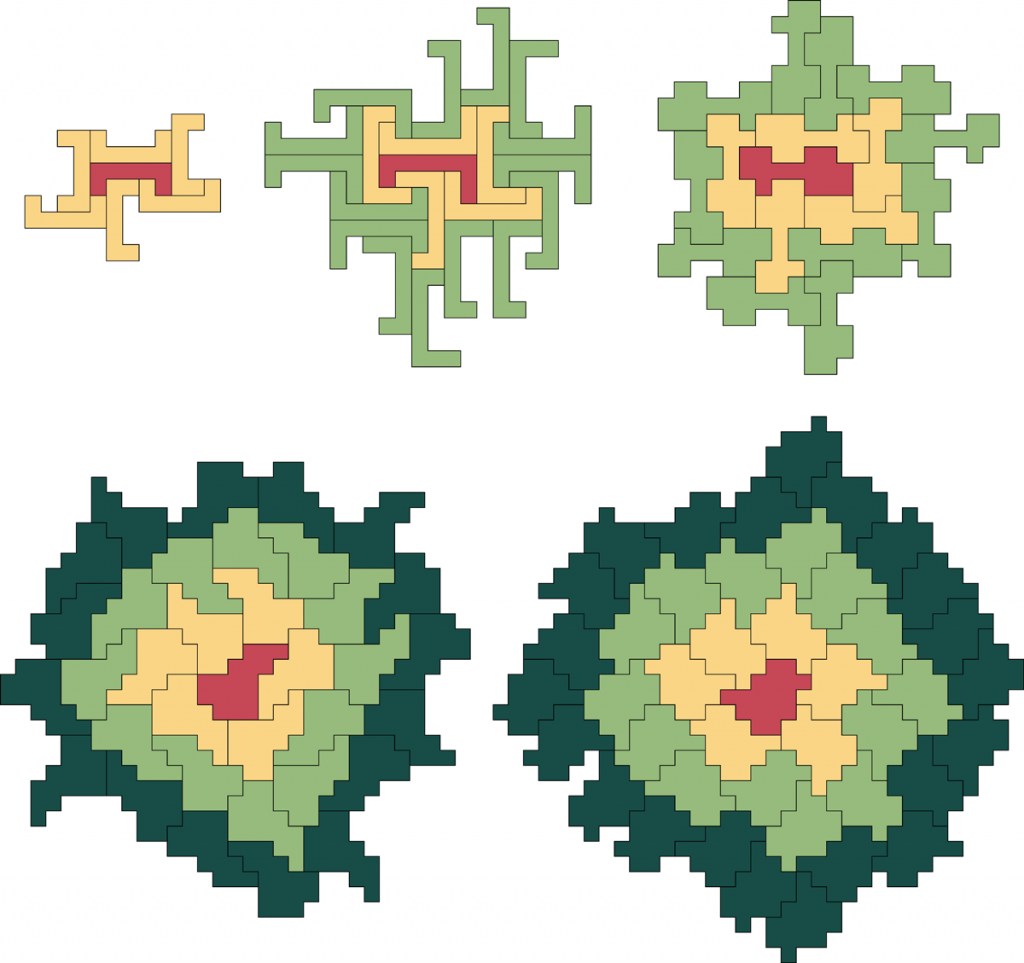
If tables of numbers make your eyes glaze over, let’s pause to look at a couple of examples. Here are some sample polyominoes with increasing Heesch numbers: a 7-omino with H = 1, a 9-omino and a 15-omino with H = 2, and two 17-ominoes with H = 3. Remember that none of these shapes tile the plane!

But wait, there’s more. Here are the Heesch numbers of hole-free polyhexes. There are a half dozen with Heesch number 4!

Heesch numbers of polyhexes, no holes in the outermost corona

n	non-tilers	H = 0	H = 1	H = 2	H = 3	H=4	Drawings
6	4		3	1			0-up
7	37	5	25	6	1		0-up
8	381	70	264	44	3		0-up
9	2717	825	1822	67	3		2-up
10	18760	8248	10234	265	13		2-up
11	116439	67644	47940	817	37	1	3-up
12	565943	431882	133484	567	10		3-up
13	3033697	2565727	466159	1783	27	1	3-up
14	14835067	13676416	1156793	1836	22		3-up
15	72633658	69871458	2758485	3534	179	2	3-up
16	356923880	350337478	6581529	4818	54	1	3-up
17	1746833634	1731652467	15167876	13129	161	1	3-up

In the drawings below, the top row shows 6-hexes with Heesch numbers 1 and 2, the 7-hex with Heesch number 3, and the 11-hex with Heesch number 4.

And completing the enumerations, here’s the table for polyiamonds, including a single example with Heesch number 4:

Heesch numbers of polyiamonds, no holes in the outermost corona

n	non-tilers	H = 0	H = 1	H = 2	H = 3	H=4	Drawings
7	1		1				0-up
8	0
9	20	11	9				0-up
10	103	44	55	3	1		0-up
11	594	236	346	11	1		0-up
12	1192	826	364	1	1		0-up
13	6290	4360	1884	24	2		2-up
14	18099	14949	3141	8			2-up
15	54808	48108	6661	39			2-up
16	159048	148881	10153	13	1		2-up
17	502366	474738	27544	83	1		2-up
18	1374593	1341460	33100	33			2-up
19	4076218	4001470	74689	57	2		2-up
20	11378831	11282686	96091	51	2	1	2-up
21	32674779	32505745	168959	73	2		2-up
22	93006494	92740453	265977	62	2		2-up
23	264720498	264216706	503651	140	1		2-up
24	748062099	747476118	585571	384	26		2-up

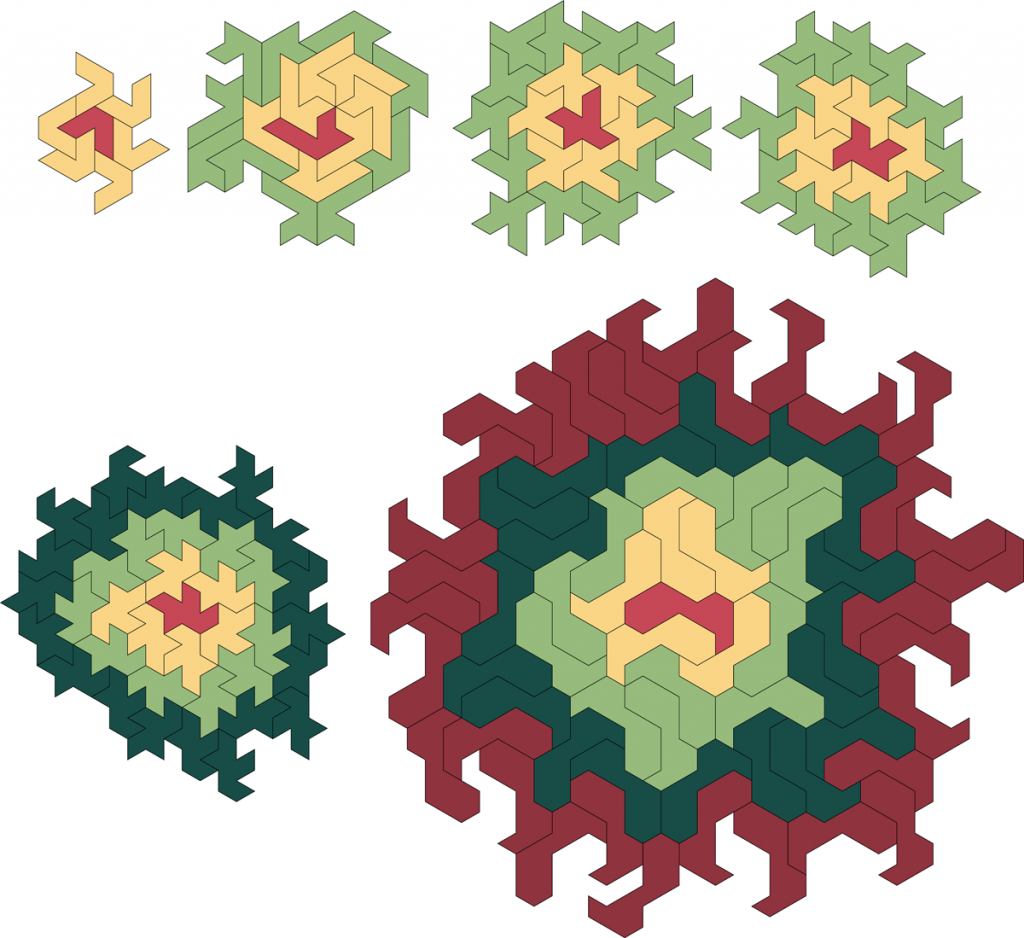
Below are the 7-iamond with Heesch number 1, three 10-iamonds with Heesch number 2, a 10-iamond with Heesch number 3, and the 20-iamond with Heesch number 4.

I’m glad these enumerations are out there in the world. Casey Mann’s work on Heesch numbers of polyforms with markings is excellent, but I felt sad for the poor unmarked polyforms, which deserved to be explored.

I might try extending the enumerations above, but I’m not excited about the prospect given that the next step for any of the polyform types will burn a lot of CPU cycles, at least without another quantum leap in performance. I’m more interested in looking for other kinds of shapes that might lead to high Heesch numbers. I have a student working on the subject with me this summer (following yet another lead suggested by Bram), so stay tuned for new results!

Comments

14 responses to “Heesch Numbers of Unmarked Polyforms”

May 26, 2021

Ivan

Couldn’t you express the existence of a hole in a corona by enumerating over all 1-ominos, 2-ominos etc and all their possible positions? For example, a cell p is a 1-hole if it’s uncovered, and all 4 neighbors of it are covered – a 5 term clause. So the existence of a 1-hole is just the union of those clauses over all cells. Now repeat for 2-ominos and all their possible transformations. I’m not sure whether adding all those might make the computation intractable, but it seems like you rarely need to worry about massive holes, so you can probably stop at some low size. It would also be a sub-formula that’s independent of the actual shape under consideration, so you would only need to construct it once.

Reply
1. May 26, 2021
  
  Craig Kaplan
  
  It’s a nice idea, but I’m afraid it is intractable in practice. There’s no a priori upper bound on the size of a hole, and while large ones are rare, they do occur in practice. So to make this work you’d have to check for every possible shape of hole in every possible position, and there are (at least) exponentially many of them.
  
  Reply
May 26, 2021

Ivan

Oh, I 100% agree that this will not reject all holes. It just seems that for the limited shape sizes and counts you are dealing with, it might improve performance by rejecting a lot of small gaps early directly through the SAT solver, by only adding a linear in board size number of terms. But this is just me guessing. In any case, a lovely paper and post, thanks for sharing!

Reply
May 26, 2021

Louis

An intriguing math puzzle with ties to both geometry and Boolean logic! Cool! Only amateur math guy talking, but take out the center ominoe and slide any loosened pieces inward: the one-hole with all but the removed piece is state 1, and the poly-hole with the piece slid is 2. Poly-hole means concave sides of the slid piece create a hole when they slide up to a flat side, while leaving behind a pocket vacated by the slide. You’ve found 2 hole structures. Can these be encoded to be found by a SAT solver ? If so, each found tiling is a generator of multiple hole structures. …

Reply
May 27, 2021

stuebinm

(apologies if this has weird line formatting or came through as a wall
of text — I’m always unsure how to properly format comments on
wordpress sites …)

Shouldn’t it be possible to avoid the problem of potential holes
entirely by modelling not the grid cells as variables, but the
edges between them? Intuitively, we can then take S to be a set
of edges of a polyomino (and again S_T as those edges under some
transformation T ∈ ), and e_p for all possible edges between
cells (set to “true” if that edge seperates two polyominos, and
to “false” if not).

Then we would have constraints like this to ensure the copies
fit together:

If we use a copy of S, then its edges are used:

S_T → e_p for all T ∈ , p ∈ T

If we use some edge, then there must be at least one and at most
two copies of S which use it (admittedly, I’ve not worked out how
to state this as a list of disjunctions, but it can be stated as
a disjunction of all cases and then transformed into CNF):

e_p → (S_A ∧ S_B ∧ ¬S_C ∧ …) ∨ (S_A’ ∧ S_B’ ∧ ¬S_C ∧ …) ∨ …

for all A,B,C ∈ with p ∈ A ∩ B ∩ C ∩ …, where A,B,C… are
pairwise distinct, and A and C are adjacent (and so on).

Additionally one would need terms that ensure the result is actually
a k-corona rather than just any pattern without holes (though I
wonder — would it be more efficient to not require that a given
position is the 0-corona, but instead try to generate as large a
tiling as possible, and find its “innermost” copy of the shape?
Though I guess “large” is difficult notion to encode in a CNF …).

I am, however, unsure if this would actually result in smaller
formulae …(though number of symbols should be identical, I think,
I’m not sure how much bringing the e_p-constraints back into CNF
would blow them up in length).

And another thought: would it be possible to “leave out” the
shape of the concrete polyomino, and ask the SAT solver something
more like “is there a n-polyomino with a k-corona”? Of course, this
would explode the “search space” that the solver may have to go
through significantly, but perhaps it would still be more efficient than
testing all possibly polyominoes? (assuming one is only interested in
existence).

Reply
1. May 27, 2021
  
  Craig Kaplan
  
  Lots of great thoughts here! Let me try to address them…
  
  1. I don’t think you gain much of anything by switching to edge variables. For all internal coronas, cell variables already capture the idea of “every cell around my boundary must be occupied”. For the outer corona, a given tile edge is allowed to have or not have a neighbouring tile, and that’s not something you can tell based purely on local information.
  
  Ultimately, holes are about *paths* of cells rather than individual cells: a cell is part of a hole if there is no path from that cell to “the cell at infinity” (or, practically, a cell on the edge of the patch’s bounding box). And there’s no a priori upper bound on how long that path can be, which makes it intractable to prevent holes purely within a SAT framework.
  
  (Also, I believe every edge variable can be expressed as a Boolean formula in terms of cell variables and shape variables. If nothing else, that shows that we don’t gain any fundamentally new information we didn’t have before.)
  
  2. Why not just generate as large a patch as possible, and find the innermost shape? It’s an interesting idea, but “large” is just such a slippery concept in this context. In effect, the whole idea of coronas is to provide a concrete (topological) meaning for “large” that doesn’t depend on the type of polyform or its precise shape. It avoids, e.g., stringing together an infinite chain of tiles without building a large blob of them.
  
  3. Could we make the SAT solver do all the work? I’ve thought about that, and while I wish such a beautiful approach could work, I suspect it’s a non-starter. First of all, the Boolean formula would need to incorporate a sub-formula that guarantees that the discovered shape doesn’t tile the plane. Given that we don’t even know all the ways shapes can tile, no such formula exists, at least not yet! Even then, you’re effectively asking the SAT Solver to write a proof of a theorem for you. At that point, you may as well accept that this is what you’re doing, and switch to proper theorem proving rather than satisfiability.
  
  Reply
August 27, 2023

Alice

Hi, I am big fan of Heesch numbers, I very like your work, I like you publish the drawings – the dataset. The pictures are so great, far beyond my imagination. The pictures make me happy. I want to see all of them, every night before sleep… Thank You…. When will you do Heesch of polykites? I saw Joseph Myers already finished list of non-tiling polykites…

Reply
1. August 27, 2023
  
  Craig Kaplan
  
  I’ve computed Heesch numbers of non-tiling polykites up to about 16- or 17-kites. Unfortunately, I haven’t found anything that interesting so far — the largest Heesch numbers I’ve seen were 2 or 3 (I can’t remember the exact details). Too bad — Polykites certainly had a strong opening, with two aperiodic monotiles early on!
  
  Reply
  1. August 29, 2023
    
    Alice
    
    May I somewhere see the result of Heesch numbers of non-tiling polykites? If not PDF drawings, I would be happy of a text file. For me, the pictures are so amazing, sometimes even Heesch 1 is enough.
    
    Reply
    1. August 30, 2023
      
      Craig Kaplan
      
      I computed a lot of Heesch numbers, but I didn’t visualize much of the results because there were no surprises. Just for fun, here’s a file containing visualizations for non-tiling 8-kites: https://cs.uwaterloo.ca/~csk/tmp/8kites.pdf. The file contains all non-tiling 8-kites with Heesch numbers greater than zero, together with three leftover shapes that were “inconclusive”. Two of the inconclusive shapes (Pages 32 and 47) are periodic but anisohedral; the one on Page 50 has become something of a celebrity :-)
      
      Reply
      1. September 1, 2023
        
        Alice
        
        Thank You, now I know, Heesch polykites look very nice. Especially, I like “little crab” on Page 30 and “falling ice-skater” on Page 39. They makes me smile. For fun, for people, it is good idea to publish more pictures (or am I the only one who like the Heesch pictures?).
        
        Tile hero on Page 50. I always call it “T-shirt” for myself, not “hat”. I still do not understand, why that simple shape waited 50 years for its discovery.
    2. November 12, 2023
      
      Anton
      
      Just getting into Heesch pictures. I’ll post some of them them here: https://www.instagram.com/antontessellations/
      
      Reply
August 1, 2024

Jens

Hello, the search for shapes with finite Heesch numbers can be expanded to the third dimension, so I experimented with different shapes in Blender (3D software). In 3D, the simplest grid is the cubic lattice. Here I found a shape with Heesch number one. By dividing a cube into six pyramids, more complex matching rules can be implemented. Interestingly, when all six pyramids point outward, we get a rhombic dodecahedron. With this, I was able to find a polyhedron with Heesch number two and one with Heesch number three. There are probably more polyhedra with finite Heesch numbers to be found by using a computer solver. Pictures are here: https://en.wikipedia.org/wiki/Heesch%27s_problem

Reply
1. August 1, 2024
  
  Craig Kaplan
  
  Thanks! Yes, a couple of people have explored the idea of using a grid of square bipyramids, i.e., the union of two of your pyramids from adjacent cubes, as a basis for constructing 3D polyforms with interesting tiling-theoretic properties. I think it’s a promising direction for exploration.
  
  For what it’s worth, I’m not a hardcore wikipedia expert, but it seems to me that putting your results directly on a Wikipedia page isn’t the best way to disseminate them. You should share your work elsewhere so that it can be vetted in a public forum (whether peer review or otherwise). Wikipedia should be the final destination for new knowledge, not its origin point.
  
  Reply

Isohedral

Heesch Numbers of Unmarked Polyforms

Computing Heesch numbers with a SAT solver

The data

Comments

14 responses to “Heesch Numbers of Unmarked Polyforms”

Leave a Reply Cancel reply