Heesch Numbers, Part 4: Edge-to-Edge Pentagons

This post is the fourth and final one in a series about Heesch numbers.  Part 1 was a general introduction, and would be a good starting point if you’re unfamiliar with the topic. Part 2 covered exhaustive computations of Heesch numbers of polyominoes and polyiamonds, and likely isn’t needed to understand this final chapter. Part 3 talked about a paper by Agaoka that presented a convex heptagon with Heesch number 1, and introduced an infinite family of new convex polygons all with Heesch number 1. It may be useful to have a look at that third instalment before reading this one.

I have one final result to share regarding Heesch numbers, but I have to say up front that it’s a bit hairy. It’ll take me a moment just to explain what the problem is. I’ll bring in a lot more technical steps—I’ll “show my work”. I’m not sure my solution will have the immediate appeal of, say, polyominoes, to anyone who isn’t already heavily invested in this topic. Still, I’ll offer this last mathematical morsel in the hopes that it inspires further work on the subject. It’s also worthwhile in that I get to drop in a digression about some exciting new developments in the world of tiling theory.

The previous post discussed a paper by Agaoka, in which he presents a convex heptagon (a seven-sided polygon) with Heesch number 1. The end of the paper contains a selection of intriguing open problems for further study. My family of “ice cream cones”, also discussed previously, lays to rest one of those problems by demonstrating the existence of -sided convex polygons with Heesch number 1 for all . Just a bit further down the page, Agaoka asks:

Is there a convex pentagon with which admits an edge-to-edge corona?

Agaoka uses to refer to the Heesch number of a shape , and his inequalities demand that the Heesch number be positive but finite. So, using the language of the previous post, he’s asking whether there’s a finitely surroundable convex pentagon that admits an edge-to-edge corona.

And what’s “edge-to-edge”? Here’s where things get a little more technical. When we place two shapes next to one another, any time a corner of one shape sits somewhere along the edge of its neighbour we’ll call the result a “T junction”. We’ll then say that a configuration of shapes is edge-to-edge when it contains no T junctions. (To be absolutely precise, it’s nicer to call such configurations “corner-to-corner”; but when all shapes are convex, as they will be here, the two concepts coincide.) Now, thinking way back, the first example I gave of a finitely surroundable shape was Heesch’s original example from 1968: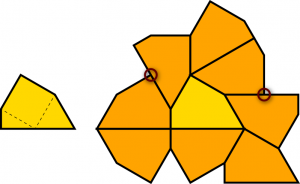

This shape is certainly a convex pentagon with Heesch number 1, but the surround shown is not edge-to-edge: two T junctions are circled. That doesn’t automatically mean that this shape is disqualified from satisfying Agaoka’s problem. It could theoretically be possible to find a different surround that avoids T junctions, and all we need is any one edge-to-edge surround to satisfy Agaoka. But as it turns out, we can show that all surrounds of Heesch’s pentagon will necessarily introduce some T junctions. On the other hand, note that Agaoka’s heptagonal bamboo shoot does admit edge-to-edge surrounds (but for record, my ice cream cones do not).

We’re left, then, with the problem of finding a convex pentagon that we can constrain enough in shape to allow it to surround itself in an edge-to-edge way, without allowing it to tile the plane. At the outset, this is a lot to ask for. Finitely surroundable shapes walk a fine line between order and disorder: they must be sufficiently well behaved that they play nicely with a ring of neighbours, without being so friendly that the first ring permits a second, a third, and so on out to infinity. But the world of convex pentagons is a already small one, making this frontier zone between order and disorder especially narrow. And asking that the surround be edge-to-edge constrains things even further.

But we do have a small advantage in this context: this world is small enough that we can easily hypothesize possible solutions and check if they actually work. Basically, imagine some possible surround for a convex pentagon. That surround will imply a set of equations that partially or fully determine the pentagon’s angles and edge lengths. If those equations have no solution then the surround can’t exist. If there is a solution, we can construct the pentagon with those angles and edge lengths and check whether it tiles the plane. If we can surround it but not tile the plane with it, we have a solution.

A promising start

At some point when pondering this problem, I started to develop a strategy based on a pentagon with three shortish edges and two longish edges, imagining a surround looking something like this: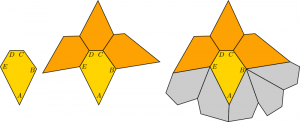The initial shape is shown on the left, with its corners labeled counterclockwise through . My thinking was that I could attach copies of the pentagon to the three short edges, leaving gaps under the resulting “wings”. Those gaps would then be filled by slotting pointy corners up into the exposed vertices. The other angles would be carefully chosen so that the two copies covering the long edges and would also touch each other, completing the surround. I aimed for two copies under the left wing and three under the right, assuming that the asymmetry would help guarantee that the shape couldn’t be too simple. Note that the diagram above is really just a sketch to guess at the arrangement of neighbours in the surround—the tiles are all different shapes. We don’t yet know whether a shape even exists that is compatible with this arrangement.

We need to copy the vertex labels to the other tiles in the surround in order to determine their orientations (the positions of the vertices are clear, but each tile may be oriented clockwise or counterclockwise). Let’s try the following configuration: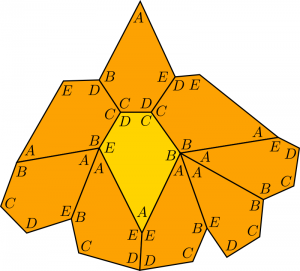The labelling makes it clear that there are only two distinct edge lengths. Because the original pentagon’s is adjacent to a neighbour’s , we know that . Similarly, . Thus we can think of this pentagon as being an isosceles triangle with a quadrilateral glued to its base. Let’s abuse the notation so that the vertex labels will also refer to the angles at those vertices, and then split the pentagon as above, dividing angle into and , and into and :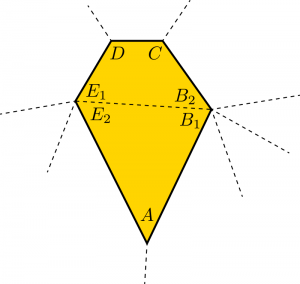From these two diagrams, we can improve our understanding of the unknown angles considerably. First, because is isosceles, we know that . But at the bottom of the proposed surround we see that we have a vertex surrounded by an and two s, from which we know . Substituting, we find that , whence . Similarly, the pentagon’s remaining surrounded vertices imply three other equations: , , and . And because is a quadrilateral, we know . With enough persistence, these equations allow us to express all angles in terms of , yielding the following cleaned-up (but still imperfect) diagram: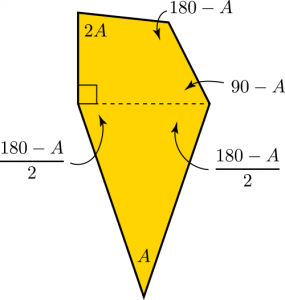Now, we’ve still got a degree of freedom that we’d eliminate in ideal circumstances, to produce a single specific value for . And it turns out that we can, if we also use what we know about the edge lengths. Let’s focus on the quadrilateral: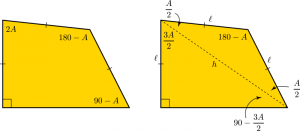We know that the three upper edges all have the same length; in particular the triangle originally labelled is isosceles. If we add a diagonal from to (and use to denote its length), we can divide up the angles as shown on the right. Using one of the angles in the right-angled triangle, some trigonometry tells us that . We can also apply the law of sines to the isosceles triangle to learn that . We can arrange that equation (and remember that ) to obtain . Equating the two derivations above at last gives us an equation purely in the unknown :

   

This is far from pretty, but I happen to have a soft spot for trigonometry. By grinding through a few fun applications of trig identities, it’s possible to deduce that

   

We thus find that , and we can use that value to solve for and . Plug all those values in, construct the pentagon, and lo and behold it can be surrounded!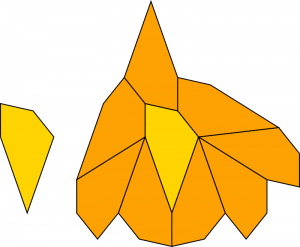So, is this the solution to Agaoka’s question that we’ve been seeking? It’s definitely convex, and definitely a pentagon. It has a surround, so its Heesch number is at least 1, and the surround shown is edge-to-edge. We need to clear one final hurdle: we need to prove that the shape doesn’t tile the plane.

How do we know whether a given convex pentagon tiles the plane? I’ve dropped hints for a while that this question is interesting. Recall that for convex polygons in general, the answer is trivial for most numbers of sides: all triangles and quadrilaterals tile the plane, and no convex -gon does for . The answer for hexagons has been understood for about a hundred years: there are three families of convex hexagons that tile, and it’s easy to check whether any given shape belongs to one of these types.

Convex pentagons have a much more colourful history. Karl Reinhardt first enumerated the three convex hexagon tiling families in 1918. In the same work, he offered a list of five types of convex pentagons that tile, but did not claim the list was complete. Over the next hundred years, an additional ten types were discovered by a mix of mathematicians and enthusiastic amateurs. (Some of these types consist of a single tile shape). The 15th type was discovered only two years ago by a team including Casey Mann, whose name has come up a few times in this series; the discovery made the rounds online as an exciting mathematical achievement. Then, earlier this year, Michaël Rao announced that he had successfully conducted an exhaustive search over all possible ways a convex pentagon could tile the plane, a search that confirmed the list of 15 types already found and didn’t turn up any new ones. I don’t believe Rao’s article has been published in a peer-reviewed forum yet, but the consensus among tiling theory researchers is that his approach is valid. In that case, we know when a given convex pentagon tiles: precisely when it belongs to one of these 15 types. It was just my good luck, then, that the one day that I could attend the CRM workshop on tilings was the day when Rao gave a talk about this work!

So, we now have a simple test for whether the pentagon proposed above satisfies Agaoka’s problem. We check it against the 15 pentagon types, and discover……that it’s a perfect match for Type 6. Dang.

Snatching victory from the jaws of defeat

So does that mean it’s game over? Not surprisingly, I wouldn’t have built up to this point if I didn’t have one final ace up my sleeve. Looking back over the construction of the previous section, there are a few places where I left behind “knobs” I can now go back and twiddle to see if I get an answer I like more. In particular, when first building a hypothetical surround, I arbitrarily chose to put two copies of the shape under what I called the “left wing”, and three copies under the “right wing”. What if we tried other values?

It turns out that for any , we can put pentagons under the left wing and pentagons under the right wing, and repeat the rest of the construction above nearly verbatim. That revised derivation eventually leads to a new quadrilateral, fortuitously similar to one that we used to solve for the angle originally: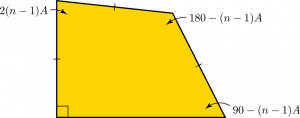Now, we could repeat the trig that allowed us to solve for , but there’s a shortcut: if we let , then we get the same angle relationships as before, now in terms of . Therefore we know that , or . From this new derivation we can construct—and surround!—a new infinite family of pentagons for all :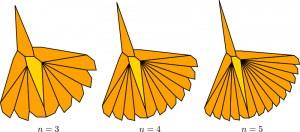I claim that these, at last, solve Agaoka’s problem. They’re convex pentagons with edge-to-edge surrounds. And for all , we can verify that they don’t tile the plane by checking against the 15 types of convex pentagons that do. As a bonus, we get an infinite family of pentagons, not just one!

It looks more specifically like all of these shapes have a Heesch number of 1. I could be wrong in two obvious ways. First, one or more of them might have a higher Heesch number. That would be amazing! I’d love to see a pentagon with a Heesch number higher than 1. And for the record, the shape would still be a win with respect to Agaoka, who wasn’t specific about the Heesch number, only that it be finite and positive. Second, if one of these shapes actually does tile the plane, that’s even more amazing! It would serve as a 16th type of tiling pentagon, and a harbinger of a flaw hidden in Rao’s exhaustive search. Both of these possibilities seem far more remote than the simple notion that I have found finitely surroundable convex pentagons with edge-to-edge surrounds, which nobody ever claimed were unlikely to exist.

Conclusion

So, that’s another of Agaoka’s problems settled, after quite a bit of scribbling. The problem that lingers most strongly in my mind is this: find a pentagon (convex or otherwise) with Heesch number 2, or prove that none can exist. More generally, if we believe Rao’s result and consider the classification of tiling convex pentagons settled, could we carry out a similar classification of non-tiling convex pentagons? That is, determine how many types there are of finitely surroundable convex pentagons, and label each type with its Heesch number. I’m not an expert on Rao’s method; perhaps it could be adapted to search for surroundability instead of tileability.

That’s also the end of this series about Heesch numbers, capturing a few new results I’ve come up with. (I may go back and update the table of Heesch numbers of polyforms if I compute more of them.) To some extent, this has been an experiment in research dissemination. I was unsure at the outset whether these results were sufficiently exciting to publish as an article in a math journal. On the other hand, I’ve always found that Heesch numbers have wide appeal to a general audience, and I enjoy the outreach component of my job a great deal. So it seemed natural to write these ideas up as a sequence of (more-or-less) accessible blog posts. I’m also interested longer term in popular writing on mathematics, and this was an opportunity to see if I could put together something in that form. Does the text work in this form? Should I create a more academic manuscript? Your feedback is welcome.

Update [October 14th, 2017]: A few weeks after publishing this note about my pentagon, I was delighted to receive a message from Teruhisa Sugimoto in Japan. It turns out that he had been working on a much more systematic and comprehensive enumeration of convex, finitely surroundable pentagons, resulting in an enumeration of 17 distinct types! My noble effort is now but one voice in a larger chorus (Category 3, to be precise). He wrote again recently to inform me that he posted a draft paper, “Convex Pentagons with Heesch Number” on his website. Sadly for me it’s in Japanese, but the diagrams tell a lovely story. Congratulations, Mr. Sugimoto!