Woven book polyhedra

Earlier this year, at a local coffee shop, I noticed a flyer on the wall with a call for artist submissions for an upcoming show in Halton Hills. The topic of the show was Altered Books. I had never experimented with the artform of altered books before, though I had seen great examples online. I resolved to devote occasional spare moments to pondering ideas for altered book sculptures—even if I didn’t end up producing something that I would be comfortable calling “art”, it might be fun to experiment.

Additional impetus came a month or two later, when by chance I discovered a lovely volume titled Art Made From Books: Altered, Sculpted, Carved, Transformed. The book was full of deeply inspiring examples by artists like Brian Dettmer (who also wrote the preface) and Guy Laramee. I knew I couldn’t live up to their standard, but wanted to try something new.

Finally, I pulled a couple of random books off the shelf, just to move them around and generate ideas. I immediately thought of a classic demonstration of friction: if you interleave the pages of two phone books, they can’t be pulled apart. (In fact, this phenomenon was in the news late last year, with the online publication of a new paper claiming to explain it with greater precision.) Of course, you don’t need to use phone books to hold two books together; even a few pages of two paperbacks will be sufficient to keep them together, as long as you don’t pull too hard.

At this point, the art-math enthusiast in me woke up and saw interleaved pages as an opportunity. Could books be used as the building blocks of polyhedral sculptures, where the interleaved pages become the means of holding the whole thing together? Once the question is asked, the answer follows in short order. A book has a built-in straight line (the spine), which wants nothing more than to play the role of an edge of a polyhedron. The book’s pages would then fan out towards the two faces adjacent to that edge, where they would interleave with the pages of books forming other edges of the same two faces. The spine would point to (but not reach) the two vertices adjacent to its edge. In some sense, each book would play the role of one edge in what computer graphics researchers call a winged-edge data structure.

The most obvious sculpture to try first is the simplest: a tetrahedron. My public library sells off unneeded paperbacks for 25 cents each, and so I was able to create this sculpture for $1.50.

That particular sculpture is titled Five Swords and a Stick, because it’s made from five dorky fantasy novels featuring burly people with swords on the cover, together with a non-fiction book about the hockey player Bobby Orr. The structure is 100% books—it holds together with no tape, (added) glue, or fasteners, and hasn’t sagged at all after about a month.

If the sculpture looks like a pain to build, that’s because it was. Every two adjacent books must have their pages interleaved manually, one by one. The interleaving becomes much more difficult as you add more books, because the sculpture closes in on itself. I didn’t keep track, but after a few initial experiments it probably took between half a day and a full day to assemble.

What’s next? After a tetrahedron, I naturally moved on to a cube, requiring 12 books. I tried to build a cube a couple of times, always unsuccessfully—basically, it kept collapsing on me. I think the problem is the faces: four books meet in a loose ring, unlike the tetrahedron, in which three books can all mutually interleave in a face. As a result, the faces didn’t really hold together.

Fortunately, there was a solid backup plan: an octahedron. As the dual of the cube, the octahedron requires the same number of books, but its triangular faces might afford it greater structural integrity. And after about a day (including some computer science, described below), I was able to produce this sculpture:

Honestly, it’s not nearly as pretty as the tetrahedron. Partly, it’s harder to fit all the pieces together cleanly and evenly. Also, the octahedron is simply bulkier. But I do like the many exposed joints where pages interleave:

Much as these sculptures should theoretically hold together based on friction alone, I cheated with the octahedron. I used tape to hold the outer covers down, and to “lock” the innermost exposed pages so that the whole thing wouldn’t start to unravel page by page. I figured I’d wait a few weeks, and if it was still holding together, I’d remove the tape. Unfortunately, the whole thing sagged quite a bit in that time:

I’ll probably dismantle the octahedron and try something else, or simply turn it into two tetrahedra.

A bit of computer science

In the process of thinking about these sculptures, I came across a genuine math problem (Linda Carson recently reminded me of Ian Stewart’s words: “A mathematician is someone who sees opportunities for doing mathematics”). I’ll finish this story with a bit of math and computer science.

If you buy a random assortment of cheap books, they’re unlikely to all have the same number of pages. And yet, it seems ideal to want to arrange them so that they interleave “cleanly”: the interleaving starts with the front and back covers on the outside, and works its way inward so that every page of every book is used. (If you look carefully, you’ll see that the tetrahedron doesn’t have this property: there are chunks of unused extra pages on the inside.) Can we choose an assignment of books to the edges of a polyhedron, and a splitting point for each of the books, so that every page gets used?

Let’s start by considering a simple case: a triangle. You have three books with , , and pages. In this case, each book will interleave with the other two. Let , and be the number of interleaved pages for each of these pairs of books. We must therefore split the pages of Book 1 so that pages are shared with Book 2, and pages are shared with Book 3, meaning that . More generally, we have a simple system of equations:

(1)  

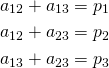
That’s three equations in three unknowns, meaning that in general you can get an exact solution to this problem! At least, notwithstanding “fractional pages” (where you can simply decide arbitrarily to assign one page to the front or back half of a given book) or “negative pages” (which will happen only when one book is longer than the other two put together).

With a polyhedron, the situation isn’t quite so rosy. We will have one known value for every edge of the polyhedron, and one value per face. Furthermore, there will be one equation per edge, based on the sum of its adjacent faces. However, a non-degenerate polyhedron will necessarily have more edges than faces, a direct consequence of Euler’s formula. That means that our system is overdetermined and we can’t count on an exact solution.

Still, we can compute a best possible solution. The usual approach in computer science is to find a set of values that minimizes the total slop in all the central book pages, in the least-squares sense. There are well-known algorithms for carrying out that computation (I used the lstsq function in Numpy).

However, that function will only tell you the best choice of values for a particular configuration of books. We might be able to achieve a lower error if we rearrange the books to produce a different set of adjacencies. At the outset there are 12! (that’s 12 factorial, or about 479 million) configurations, but we can fix one edge and deal only with the other 11! (around 40 million) configurations. We could use symmetry considerations to go even smaller, but at this point laziness prevails: I can compute 40 million least-square solutions in an hour or two without sweating over symmetries. Question for the theoreticians: is there a faster way to find the best least-squares solution over all permutations of the books? To me, this question has overtones of an NP-Hard problem, but I haven’t pursued the question.

In the end, for the 12 books I used my program found a solution with an error of about 28 total pages, meaning that there were roughly two or three pages of slop per book in the centre of the sculpture. That’s basically unnoticeable (or easily concealed by skipping a page somewhere in the middle of the interleaved bundles).

Finally, we might address the question of marketing. A natural pun-based name for these sculptures is “Bookyballs”. Patrick Honner suggested the term “sheafing” for the process of interleaving pages in this manner. I welcome other suggestions. And of course, I’d love to hear about it if you attempt any sculptures of your own using this technique.