This is the third post in a planned series of four about Heesch numbers. In the first post, I introduced some of the basic ideas behind Heesch numbers; if you’re not familiar with the topic, you may want to read it before coming back here. The second post was about Heesch numbers of simple polyforms like polyominoes; the ideas presented here will not depend on it.
Earlier this year, the CRM, a math research institute at the Université de Montréal, held a two-week session entitled “Combinatorics on Words and Tilings“. Because of ridiculous scheduling constraints, I was able to attend for one day. Thus it was that I found myself taking a full-day train ride on Tuesday, attending the workshop on Wednesday, and taking the train home on Thursday. Mind you, there was a side benefit: I was able to spend the evenings with my parents and brother in Montreal, and belatedly celebrate my parents’ 50th anniversary. And happily, it turns out that I chose a good day to be present at the workshop; more on that in the next post.
Also happily, I ended up spending most of the day sitting next to tiling theorist Casey Mann. Casey is the current Heavyweight Champion of Heesch numbers, having found the 5-hexapillar with Heesch number 5 that I showed previously.
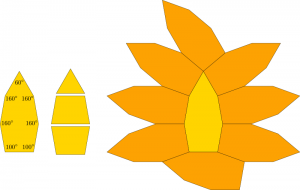
As part of our idle conversation, Casey introduced me to a lovely short paper I hadn’t seen before: “An example of convex heptagon with Heesch number one” by Yoshio Agaoka. Responding to an earlier conjecture that every convex heptagon (7-sided polygon) would necessarily have Heesch number 0, Agaoka introduces the following shape, which he calls a “bamboo shoot”:
Agaoka claims that this shape has Heesch number 1. In fact, it’s not too hard to see why this must be so. First, unless I’m perpetrating a vicious deception, the configuration above shows that the Heesch number is at least 1, so we must simply convince ourselves that it could not be higher.
Note first that this shape definitely can’t tile the plane. Here, we can make use of one of my all-time favourite facts in tiling theory, one that I take great pleasure in repeating: no convex polygon with more than six sides can tile the plane, period! How can we possibly know so much about a shape’s capabilities based only on its number of sides? The theorem ultimately boils down to a variation on one of the most famous formulas in geometry: Euler’s formula. You know, V – E + F = 2, where V, E, and F are the numbers of vertices, edges, and faces, respectively, in a polyhedron. It turns out that the same formula holds in the plane, and further can be adapted to hold for an infinite tiling as the limit of ever-larger finite chunks of that tiling. In this case, if you tried to tile the plane with a convex polygon with more than six sides, you’d find that you were laying down too many new vertices to surround them all with tiles, a deficit that cannot be reversed as a patch of tiles grows to cover the whole plane. (On the other hand, a non-convex polygon can mate with a neighbour along many edges at the same time, potentially sidestepping this issue.) I find this theorem both astounding and infuriating—nobody’s going to tell me what I can and can’t do with a convex polygon!—and yet there it is, buried somehow deep in the firmware of the Euclidean plane. It also nearly settles the question of which convex polygons tile the plane. We know that all 3-gons and 4-gons do, and now we know that no n-gons tile for n ≥ 7. That leaves just 5 and 6; more about them in the next post.
Knowing that the bamboo shoot doesn’t tile means it’s already guaranteed to be interesting, because its Heesch number is positive but finite. For convenience, let’s call such shapes finitely surroundable. In the search for high Heesch numbers, finitely surroundable shapes are guaranteed to be at least somewhat interesting stops along the way.
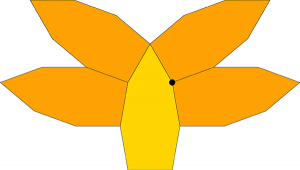
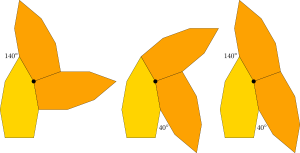
Agaoka completes his proof by noting that any legal surround of the bamboo shoot must contain at least these four neighbours:It’s possible to deduce the necessity of this configuration by remembering that the material that surrounds each vertex must add up to 360°. Consider the marked vertex above, for example. The bamboo shoot has an angle of 160° there; we must make up the other 200° using some combination of 60, 100, and 160 (the bamboo shoot’s angles) and 180 (which you can achieve by having a polygon edge partially overlap the vertex). It’s easy to see that the only possible solution is two 100° vertices. There are four ways to position adjacent shoots to cover this vertex, but the other three would lead to subsequent gaps of 140° or 40° at neighbouring vertices, neither of which can be closed off:It’s then possible to work from the legal partial surround above to figure out all possible ways to fully surround the central shape. Moreover, note that the two side-by-side orange tiles making up one of the “wings” leave behind another angle of 40°, meaning that none of these legal surrounds will itself be surroundable. Thus the Heesch number must be precisely 1.
Best of all, Agaoka ends his paper with a few additional unsolved problems. Among them, he asks a natural follow-up question: does there exist a convex octagon with Heesch number 1? In the rest of this post, I will answer a generalization of this question, and describe a family of shapes {Sn }, where each shape Sn is a convex polygon with n sides that has Heesch number 1 when n ≥ 7.
The sides of the bamboo shoot suggest a way forward: let’s imagine that part of a shape will be an “arc” of short sides. Opposite them will be a single additional short side that allows a “fan” of copies of the shape to be placed along the arc. We end up with a shape that looks a bit like… an ice cream cone? In any case, we’re looking for a configuration that looks something like this:
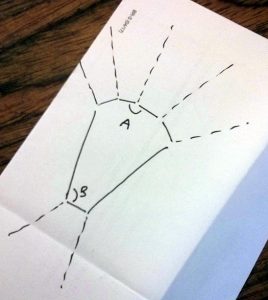
The sketch shows a heptagon, but let’s assume we’re working more generally with an n-sided polygon, so that the arc will consist of n – 3 short edges. The rest of the polygon will consist of a single short edge sandwiched between two long edges. We’ll further assume that the angles at the ends of the arc, where the short edges meet the long edges, are also A. In that case, we already know enough to solve for the marked angles A and B in the drawing, based on two equations:
![]()
![]()
The first equation simply says that it should be possible to surround a vertex by an A and two Bs. The second equation recognizes the the interior angles of an n-sided polygon must total 180(n-2) degrees. Substituting and solving, we find that
![]()
If we fix the short edges to have unit length, then a bit of annoying trigonometry is required to compute the lengths of the long edges, but it’s pretty easy to write a program that solves for the edge length numerically. I’ll omit the details.
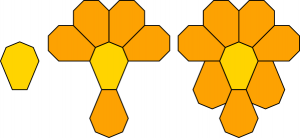
The result for n = 7 looks like the shape on the left below.The middle diagram shows a partial surround in which we use up all the short edges, as planned. But the best part is that the gaps left behind along the long edges can be precisely filled with two more copies of the shape, yielding a complete surround, as shown on the right (note that all of the original shape’s vertices end up surrounded by two Bs and an A). We know this shape can’t tile, and so it’s already guaranteed to be finitely surroundable (i.e., interesting!). Could it have Heesch number 2? By examining possible ways to sum angles to 360°, it’s possible to convince oneself that no surround of the central shape can be further surrounded—you’ll always leave behind unfillable acute angles as in the right-hand diagram above. The details are a bit boring, but if you want you can read my sketch proof. (Of course, I wouldn’t mind if one of these shapes could be further surrounded, as it means its Heesch number is 2 or higher!)
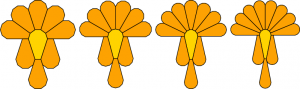
There’s nothing about the previous discussion that’s tied to the fact that the shape had 7 sides, and indeed, this construction generalizes to all higher numbers, yielding an infinite family of convex polygons, all with Heesch number 1. Here are the corresponding configurations for shapes with 8, 9, 10 and 11 sides:
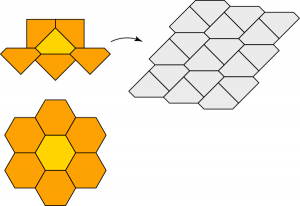
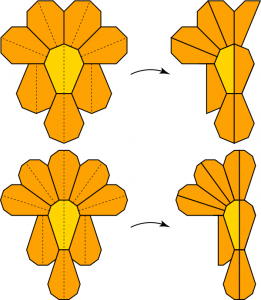
The construction definitely doesn’t work for 5 and 6 sides: it produces shapes that tile the plane (most obviously, the construction for 6 sides yields a regular hexagon):But if we want to be sneaky, we can piggyback on this technique to invent a new pentagon and a new hexagon that have Heesch number 1. All we have to do is take one of the larger shapes above and divide it in half. Because the shape is symmetric, the two halves will be congruent, and so we already know that we’ll have at least as much surroundability as we had previously. The diagrams below show the construction of a pentagon from half of a heptagon, and a hexagon from half of an octagon.Here I’m being a bit cavalier mathematically. Perhaps other surrounds could be found for one of these shapes that permit additional layers of tiles, and hence higher Heesch numbers. Indeed, because the shapes on the right have fewer than 7 sides, we can’t even automatically assume they don’t tile. Can we prove they don’t tile by other means? As I said above, pentagons and hexagons are the only convex polygons for which we don’t have an immediate yes/no answer regarding tileability. Are there special rules that hold in these two cases? I’ll say a bit more about that next time. In the meantime, I’m confident that these sliced shapes both work as advertised, though I’ll retain a modicum of doubt.
The good news here, then, is that we appear to have a piece of genuinely new math: an infinite family of convex polygons, all with Heesch number 1. Having unlocked this particular achievement, I suppose I’ll finish by taking the opportunity to pose my own problem: find a convex polygon with Heesch number 2. Unless I’m mistaken, no such polygon is currently known.
Update [November 12th, 2018]: I recently received an email from Alexander Thomas, a mathematics PhD student at IRMA in Strasbourg. He wrote to tell me that when he was still in high school he also studied some of these same problems together with Christopher Standke, and found a different family of convex ![]() -gons with Heesch number 1 for all
-gons with Heesch number 1 for all ![]() . His report is written in German, but the diagrams make it pretty clear that he has a working solution (see especially Pages 31–35). Nice work!
. His report is written in German, but the diagrams make it pretty clear that he has a working solution (see especially Pages 31–35). Nice work!


Leave a Reply to Jordan Stile Cancel reply