The photo above is a paper model of a polyhedron that I just assembled. The model consists of four dodecagons (12-sided regular polygons) and 12 decagons (10-sided regular polygons). The holes are 28 equilateral triangles that in theory could be filled with more paper.

This polyhedron has a few symmetries, and it’s customary in such cases to show additional views along the main symmetry axes. As it happens, this model has two distinct flavours of threefold rotational axes, and one family of twofold axes.

To construct this paper model, I cut the faces out of card stock using a digital craft cutter (a QuicKutz Silhouette that I bought many years ago). These are great, inexpensive tools for cutting paper; the decagons and dodecagons are about as precise as I could possibly get from pieces of paper, and fast to cut once I got them drawn in Adobe Illustrator.

Unfortunately, there’s a small problem with this polyhedron: it doesn’t exist. Mathematically, you can prove that if you want all the faces to be regular polygons, there’s no way that these shapes will close up into a perfect solid. Proving this fact from first principles would be pretty annoying. The much simpler (and less satisfying) way to prove it is to check the cheat sheet. Mathematicians proved about fifty years ago that if a polyhedron is convex and has regular polygons as faces, then it has to be a Platonic solid, an Archimedean solid, a prism, an antiprism, or a Johnson solid. This proposed solid doesn’t appear in any of those lists, and so there must be something wrong with it (there’s absolutely no reason to believe that any of those lists are incomplete, so I don’t suggest you start trying to extend them).

What’s wonderful, though, is that despite this shape’s impossibility, it does a pretty good job of masquerading as a Johnson solid. Mathematics tells me that there must be some error in my construction, but that error is diffused over all the whole model. It takes the form of a bit of paper buckling over here, a bit of slack in the tape between two faces over there, and so on. The error is small enough that if you didn’t have the cheat sheet, you might assemble the model out of paper and convince yourself that this is a real polyhedron.

This sort of polyhedron is sometimes called a near-miss Johnson solid. There’s some theoretical realization of the polyhedron in which the faces are slightly irregular, but the irregularity is so small that you’d never notice it if you were working with paper. Or, put another way, the real, mathematical error inherent in the solid is comparable to the practical error that comes from working with real-world materials and your imperfect hands. There’s no comprehensive list of near-miss Johnson solids; in fact, there isn’t really a rigorous definition of them. Any such definition would probably have to include some kind of threshold, a  measure of how far you are from regularity. But what should we measure, and how are we allowed to move error around? It’s a fussy question. Still, people have assembled a few lists of interesting examples. The most comprehensive list was curated by Jim McNeill; I have a very old web page with a few more.

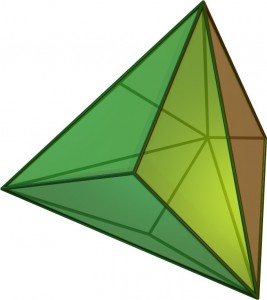
As far as I know, there’s no systematic way to construct near misses—you just have to stumble across them. In the case of the solid above, I can explain how I discovered it. I had been playing with a shape called the triakis tetrahedron, which looks like a tetrahedron with shallow pyramids built on each triangular face:

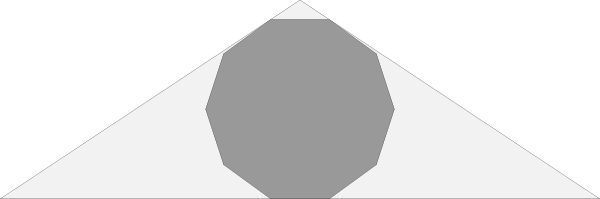
This solid has 12 obtuse isosceles triangles as faces. By fiddling around in Adobe Illustrator, I noticed that I could place a regular decagon in each of those faces, in such a way that the edges of the decagon lined up roughly with the edges of the triangle. In the diagram below, notice that the bottom edge is flush with the triangle, but the edges at the top don’t quite line up. Still, it’s pretty close.

So, imagine drawing these decagons on every face of the triakis tetrahedron, and then deleting the underlying tetrahedron. You’d get 12 decagons that roughly fit together in a loose web. What’s cool, though, is that the large empty spaces near the sharp corners of the original solid would each be surrounded by six decagons in a way that can just about accommodate the dodecagons. That’s what I noticed by constructing a couple of lo-fi paper models:

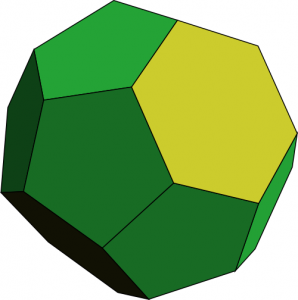
There’s actually another way to construct this same solid, via an existing near miss. Go back to the triakis tetrahedron, and slice off a bit from each of the four sharp corners. Those corners turn into regular hexagons. And if you slice at the right depth, the leftover bits look a bit like pentagons:

Jim McNeill has this solid catalogued as Number 22 in his list. My near miss can be seen as a simple modification of this one, in which you now do more slicing, this time at every vertex. The vertices are all threefold, giving you a bunch of new triangles; in the process, the pentagons and hexagons turn into decagons and dodecagons. In that light, perhaps we shouldn’t regard my new solid as especially novel, but it was still fun to conjure out of the mathematical ether.

I love the topic of near misses. It’s great to discover these new oddball polyhedra. But more generally, the idea of near misses extends to other parts of mathematics. Consider, for example, the two approximate compass and straightedge constructions of regular pentagons discussed in an article by Raul A. Simon (attributed to everyone’s favourite renaissance thinkers, Leonardo da Vinci and Albrecht Dürer). Those constructions are similar to near-miss Johnson solids: the mathematical error in the construction is comparable to the error of paper, pen, compass, straightedge and hands, so that you might not notice that you were drawing a slightly irregular pentagon. Where else in mathematics or beyond it might we find near misses, once we adopt this mindset?